题目内容
（2012•盐城一模）[选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．A．（选修4-1：几何证明选讲）如图，⊙O的半径OB垂直于直径AC，D为AO上一点，BD的延长线交⊙O于点E，过E点的圆的切线交CA的延长线于P．
求证：PD2=PA•PC．
分析：先证明PD=PE，再根据PE切⊙O于点E，利用切割线定理可得PE2=PA•PC，从而问题得证．
解答：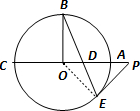
证明：连接OE，因为PE切⊙O于点E，所以∠OEP=90°，
所以∠OEB+∠BEP=90°，
因为OB=OE，所以∠OBE=∠OEB，
因为OB⊥AC于点O，所以∠OBE+∠BDO=90°…（5分）
故∠BEP=∠BDO=∠PDE，PD=PE，
又因为PE切⊙O于点E，所以PE2=PA•PC，
故PD2=PA•PC…（10分）
证明：连接OE，因为PE切⊙O于点E，所以∠OEP=90°，所以∠OEB+∠BEP=90°，
因为OB=OE，所以∠OBE=∠OEB，
因为OB⊥AC于点O，所以∠OBE+∠BDO=90°…（5分）
故∠BEP=∠BDO=∠PDE，PD=PE，
又因为PE切⊙O于点E，所以PE2=PA•PC，
故PD2=PA•PC…（10分）
点评：圆的切线性质是圆的切线垂直于经过切点的半径，遇到切线方程，连接半径是我们常用的方法．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
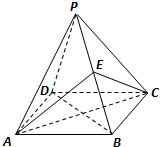（2012•盐城一模）如图，在四棱锥P-ABCD中，四边形ABCD是菱形，PA=PC，E为PB的中点．