题目内容
4.已知函数f(x)=$\frac{1}{2}$x2-(a2-a)1nx-x(a≤$\frac{1}{2}$).(1)当a=-1时,求函数y=f(x)的极值;
(2)讨论函数f(x)的单调性;
(3)设g(x)=a2lnx2-x,若f(x)>g(x)对?x>1恒成立.求实数a的取值范围.
分析 (1)f(x)=$\frac{1}{2}$x2-21nx-x的定义域为(0,+∞),再求导f′(x)=x-$\frac{2}{x}$-1=$\frac{(x-2)(x+1)}{x}$,从而判断函数的单调性,再求极值;
(2)求导f′(x)=x-$\frac{{a}^{2}-a}{x}$-1=$\frac{(x-a)(x+(a-1))}{x}$,讨论以确定导数的正负,从而确定函数的单调性;
(3)化简可得$\frac{1}{2}$x2-(3a2-a)1nx>0,从而可得6a2-2a<$\frac{{x}^{2}}{lnx}$,令F(x)=$\frac{{x}^{2}}{lnx}$,从而求得Fmin(x)=F($\sqrt{e}$)=2e;从而化为3a2-a-e<0,从而解得.
解答 解:(1)当a=-1时,f(x)=$\frac{1}{2}$x2-21nx-x的定义域为(0,+∞),
f′(x)=x-$\frac{2}{x}$-1=$\frac{(x-2)(x+1)}{x}$,
故f(x)在(0,2)上单调递减,在(2,+∞)上单调递增,
故f(x)在x=2处取得极小值f(2)=2-2ln2-2=-ln4;
(2)∵f(x)=$\frac{1}{2}$x2-(a2-a)1nx-x,
∴f′(x)=x-$\frac{{a}^{2}-a}{x}$-1=$\frac{(x-a)(x+(a-1))}{x}$,
①当a=$\frac{1}{2}$时,f′(x)≥0恒成立,
故f(x)在(0,+∞)上单调递增,
②当0<a<$\frac{1}{2}$时,
f(x)在(0,a),(1-a,+∞)上单调递增,
在(a,1-a)上单调递减,
③当a≤0时,
f(x)在(0,1-a)上单调递减,(1-a,+∞)上单调递增;
(3)∵f(x)>g(x),
∴$\frac{1}{2}$x2-(a2-a)1nx-x>a2lnx2-x,
即$\frac{1}{2}$x2-(3a2-a)1nx>0,
即6a2-2a<$\frac{{x}^{2}}{lnx}$,
令F(x)=$\frac{{x}^{2}}{lnx}$,则F′(x)=$\frac{x(2lnx-1)}{(lnx)^{2}}$,
故F(x)在(1,$\sqrt{e}$)上是减函数,在($\sqrt{e}$,+∞)上是增函数,
故Fmin(x)=F($\sqrt{e}$)=2e;
故6a2-2a<2e,
故3a2-a-e<0,
故$\frac{1}{6}$(1-$\sqrt{1+12e}$)<a<$\frac{1}{6}$(1+$\sqrt{1+12e}$).
点评 本题考查了导数的综合应用及分类讨论的思想应用,同时考查了恒成立问题.

| A. | $\frac{\sqrt{5}}{3}$ | B. | -$\frac{\sqrt{5}}{3}$ | C. | ±$\frac{\sqrt{5}}{3}$ | D. | 以上都不对 |
| 班级 | 1班 | 2班 | 3班 | 4班 |
| 人数 | 2 | 3 | 1 | 4 |
(2)记这3人中来自2班的人数为X,求X的分布列和数学期望.
| A. | 24 | B. | 36 | C. | 48 | D. | 60 |
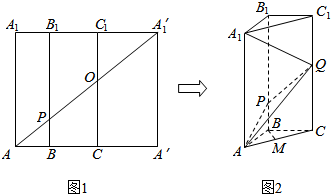 如图1所示:在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA${\;}_{1}^{′}$分别交BB1、CC1于P,Q两点,将正方形沿BB1、CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
如图1所示:在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA${\;}_{1}^{′}$分别交BB1、CC1于P,Q两点,将正方形沿BB1、CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.