题目内容
8.△ABC中,BC=2,∠ABC=θ.(Ⅰ)若cos$\frac{θ}{2}$=$\frac{2\sqrt{5}}{5}$,AB=5,求AC的长度;
(Ⅱ)若∠BAC=$\frac{π}{6}$,AB=f(θ),求f(θ)的最大值.
分析 (Ⅰ)根据余弦的倍角公式求出cosθ,由余弦定理即可求AC的长度;
(Ⅱ)求出角C的大小,根据正弦定理表示出f(θ),根据三角函数的性质即可取出f(θ)的最值.
解答 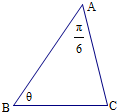 解:(Ⅰ)若cos$\frac{θ}{2}$=$\frac{2\sqrt{5}}{5}$,则cosθ=2cos2$\frac{θ}{2}$-1=2×($\frac{2\sqrt{5}}{5}$)2-1=$\frac{3}{5}$,
解:(Ⅰ)若cos$\frac{θ}{2}$=$\frac{2\sqrt{5}}{5}$,则cosθ=2cos2$\frac{θ}{2}$-1=2×($\frac{2\sqrt{5}}{5}$)2-1=$\frac{3}{5}$,
∵AB=5,BC=2,
∴由余弦定理可得AC2=AB2+BC2-2AB•BCcosθ=25+4-2×5×2×$\frac{3}{5}$=17,
故AC=$\sqrt{17}$.
(Ⅱ)若∠BAC=$\frac{π}{6}$,AB=f(θ),
则C=π-$\frac{π}{6}$-θ=$\frac{5π}{6}$-θ,
则由正弦定理得$\frac{AB}{sin(\frac{5π}{6}-θ)}$=$\frac{BC}{sin\frac{π}{6}}$,
即AB=f(θ)=$\frac{2}{\frac{1}{2}}$•sin($\frac{5π}{6}$-θ)=4sin($\frac{5π}{6}$-θ),
则当$\frac{5π}{6}$-θ=$\frac{π}{2}$,即θ=$\frac{π}{3}$时,
f(θ)取得最大值,最大值为4.
点评 本题主要考查解三角形的应用,根据正弦定理和余弦定理是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知F为抛物线C:y2=4x的焦点,点E在C的准线上,且在x轴上方,线段EF的垂直平分线与C的准线交于点Q(-1,$\frac{3}{2}$),与C交于点P,则点P的坐标为( )
| A. | (1,2) | B. | (2,2$\sqrt{2}$) | C. | (3,2$\sqrt{3}$) | D. | (4,4) |
19.已知a=$\int_0^{\frac{π}{2}}{(-cosx)dx}$,则${({ax+\frac{1}{2ax}})^9}$展开式中,x3项的系数为( )
| A. | $\frac{63}{8}$ | B. | $\frac{63}{16}$ | C. | $-\frac{21}{2}$ | D. | $-\frac{63}{8}$ |
3.在边长为2的正方形ABCD中,E,F分别为BC和DC的中点,则$\overrightarrow{DE}$•$\overrightarrow{BF}$=( )
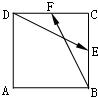

| A. | -$\frac{5}{2}$ | B. | $\frac{3}{2}$ | C. | -4 | D. | -2 |
13.“x>2”是“2x>x2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |