题目内容
11. (两选一)
(两选一)(1)一同学在电脑中打出如下图若干个圆(○表示空心圆,●表示实心圆)
○●○○●○○○●○○○○●○○○○○●○…
问:到2006个圆中有61 个实心圆.
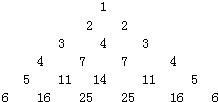
(2)如图,它满足①第n行首尾两数均为n,②表中的递推关系类似杨辉三角,则第n行(n≥2)第2个数是$\frac{{n}^{2}-n+2}{2}$.
分析 (1)本题可依次解出空心圆个数n=1,2,3,…,圆的总个数.再根据规律,可得出前2006个圆中,实心圆的个数;
(2)依据“中间的数从第三行起,每一个数等于它两肩上的数之和”则第二个数等于上一行第一个数与第二个数的和,即有an+1=an+n(n≥2),再由累加法求解即可.
解答 解:(1)∵n=1时,圆的总个数是2;
n=2时,圆的总个数是5,即5=2+3;
n=3时,圆的总个数是9,即9=2+3+4;
n=4时,圆的总个数是14,即14=2+3+4+5;
…;
∴n=n时,圆的总个数是2+3+4+…+(n+1).
∵2+3+4+…+62=1952<2006,2+3+4+…+63=2015>2006,
∴在前2006个圆中,共有61个实心圆.
(2)依题意an+1=an+n(n≥2),a2=2
所以a3-a2=2,a4-a3=3,…,an-an-1=n
累加得 an-a2=2+3+…+(n-1)=$\frac{(n-1)(n+1)}{2}$
∴an=$\frac{{n}^{2}-n+2}{2}$
故答案为:61;$\frac{{n}^{2}-n+2}{2}$.
点评 本题是一道找规律的题目,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
2.菱形的对角线相等,正方形是菱形,所以正方形的对角线相等.在以上三段论的推理中( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 结论错误 |
3.平行四边形、矩形、菱形、正方形都具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线相等 | D. | 对角线互相垂直且相等 |
20.从6名同学中选出2名参加某一项活动,有( )种不同的选法.
| A. | 30 | B. | 36 | C. | 15 | D. | 40 |
1.给出如图的程序框图,那么输出的数是( )


| A. | 2450 | B. | 2550 | C. | 4900 | D. | 5050 |
 若电视塔AB的高度为30米,且在D,C两点的仰视角分别为45度和60度,且∠DBC=30°,则C,D两点间的距离是多少米.
若电视塔AB的高度为30米,且在D,C两点的仰视角分别为45度和60度,且∠DBC=30°,则C,D两点间的距离是多少米.