Question

【题目】已知为椭圆上的一点，F为椭圆的右焦点，且垂直于x轴，不过原点O的直线交椭圆于A，B两点，线段的中点M在直线上.

（1）求椭圆C的标准方程；

（2）当的面积最大时，求直线的方程.

Answer 1

【答案】（1）（2）

【解析】

（1）根据题意计算得到，，得到椭圆方程.

（2）设，，设直线，代入椭圆的方程得到，，计算，设，求导得到最值.

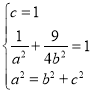（1）设椭圆的半焦距为，由题知，解得，.

所以椭圆C的标准方程为.

（2）因为不过原点O的直线交椭圆于A，B两点，线段的中点M在直线上，所以直线的斜率存在且不为0.

设，，则.

设直线，代入椭圆的方程整理得（*），

则，，故.

又，所以.

将k的值代入（*）式即得，故，，

且，即或.

，

点到直线的距离为，所以.

令，或，求导得.

令，解得.

当时，，函数为增函数；当，时，，函数为减函数，所以当时，的面积取得最大值.

综上，当的面积取得最大值时，直线的方程为，即.