题目内容
在平面直角坐标系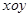 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(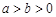 ,
,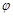 为参数),在以
为参数),在以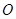 为极点,
为极点,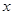 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线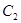 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线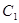 上的点
上的点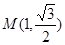 对应的参数
对应的参数 ,射线
,射线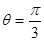 与曲线
与曲线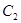 交于点
交于点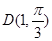 .
.
(I)求曲线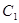 ,
,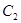 的方程;
的方程;
(II)若点 ,
,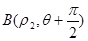 在曲线
在曲线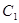 上,求
上,求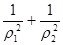 的值.
的值.
(I)曲线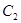 的方程为
的方程为 ,或
,或 .
.
(II)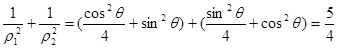
解析试题分析:(I)将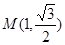 及对应的参数
及对应的参数 ,代入
,代入 ,
,
得 ,即
,即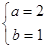 ,
,
所以曲线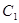 的方程为
的方程为 (
(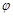 为参数),或
为参数),或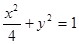 .
.
设圆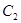 的半径为
的半径为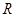 ,由题意,圆
,由题意,圆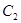 的方程为
的方程为 ,(或
,(或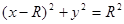 ).
).
将点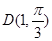 代入
代入 , 得
, 得 ,即
,即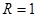 .
.
(或由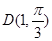 ,得
,得 ,代入
,代入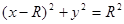 ,得
,得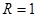 ),
),
所以曲线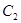 的方程为
的方程为 ,或
,或 .
.
(II)因为点 ,
,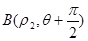 在在曲线
在在曲线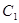 上,
上,
所以 ,
,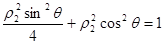 ,
,
所以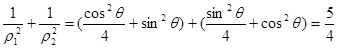
考点:本题主要考查简单曲线的极坐标方程,直角坐标与极坐标的互化,参数方程与普通方程的互化。
点评:中档题,此类问题往往不难,解的思路比较明确。(3)是恒等式证明问题,利用点在曲线上,得到 ,
,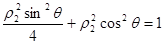 ,从中解出
,从中解出 ,
, ,利用三角函数“平方关系”,达到证明目的。
,利用三角函数“平方关系”,达到证明目的。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,曲线
中,曲线 的参数方程为
的参数方程为 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线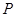 的方程为
的方程为 .
. 、
、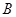 ,求
,求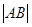 .
. 的极坐标方程是
的极坐标方程是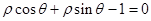 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,在曲线
轴的正半轴,建立平面直角坐标系,在曲线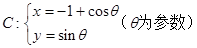 上求一点,使它到直线
上求一点,使它到直线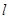 的距离最小,并求出该点坐标和最小距离
的距离最小,并求出该点坐标和最小距离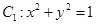 ,将
,将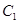 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的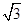 、2倍后得到曲线
、2倍后得到曲线 . 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
. 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线 .
.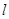 的直角坐标方程和曲线
的直角坐标方程和曲线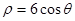 ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为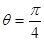 ,曲线C1,C2相交于A,B两点
,曲线C1,C2相交于A,B两点
 ,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值.
,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值. 中,直线l的参数方程为:
中,直线l的参数方程为: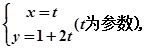 在以O为极点,以x 轴的正半轴为极轴的极坐标系中,圆C的极坐标方程为:
在以O为极点,以x 轴的正半轴为极轴的极坐标系中,圆C的极坐标方程为: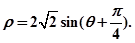
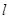 与圆C的位置关系.
与圆C的位置关系. 。
。 的参数方程化为普通方程;
的参数方程化为普通方程;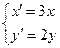 后得到曲线
后得到曲线 ,求曲线
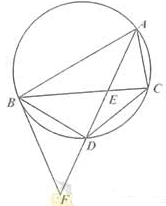
,求曲线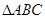 是圆的内接三角行,
是圆的内接三角行, 的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分
的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分 ;②
;② ;③
;③ ;④
;④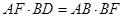 .则所有正确结论的序号是( )
.则所有正确结论的序号是( )