题目内容
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,现将
的中点,现将![]() 与
与![]() 折起,使得平面
折起,使得平面![]() 及平面
及平面![]() 都与平面
都与平面![]() 垂直.
垂直.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.

【答案】(1)见解析(2)![]()
【解析】分析:(1)分别取![]() 中点
中点![]() ,分别连接
,分别连接![]() ,可证明
,可证明![]() 平面
平面![]() 平面
平面![]() ,可得
,可得![]() ,又
,又![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,![]() ,从而可得
,从而可得![]() 平面
平面![]() ;(2)以
;(2)以![]() 为原点,
为原点,![]() 为
为![]() ,
,![]() 正半轴,建立空间直角坐标系,可得平面
正半轴,建立空间直角坐标系,可得平面![]() 的一个法向量
的一个法向量![]() ,利用向量垂直数量积为零列方程组求出平面
,利用向量垂直数量积为零列方程组求出平面![]() 的法向量,由空间向量夹角余弦公式可得结果.
的法向量,由空间向量夹角余弦公式可得结果.
详解:(1)分别取![]() 中点
中点![]() ,分别连接
,分别连接![]() ,则
,则![]() 且
且![]()
∵平面![]() 及平面
及平面![]() 都与平面
都与平面![]() 垂直,
垂直,
∴![]() 平面
平面![]() 平面
平面![]() ,
,
由线面垂直性质定理知![]() ,又
,又![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,![]()
又![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)如图,以![]() 为原点,
为原点,![]() 为
为![]() ,
,![]() 正半轴,建立空间直角坐标系
正半轴,建立空间直角坐标系![]() ,则
,则![]() .
.
平面![]() 的一个法向量
的一个法向量![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,
,
则 ,取
,取![]() 得
得![]()
∴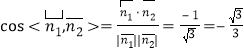 ,
,
注意到此二面角为钝角,
故二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
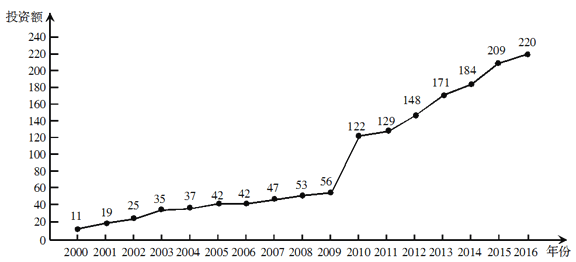
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?