题目内容
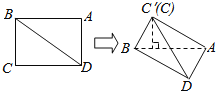
【题目】如图所示，在矩形ABCD中，
，
沿对角线将
折起，使点C移到
点，且C点在平面ABD的射影O恰在AB上．
(1)求证：
平面ACD；
求直线AB与平面
D所成角的正弦值．
【答案】（1）详见解析；（2）
.
【解析】
(1）由已知条件推导出DA⊥BC，BC⊥DC，由此能证明BC⊥平面ACD．
（2）作AM⊥DC于M，由已知条件推导出∠ABM是AB与平面BCD所成的角，由此能求出直线AB与平面BCD所成角的正弦值．
证明：
在矩形ABCD中，
，
平面ABD，AB是BC在平面ABD内的射影，
，
，
又
，
平面ACD．
解：作
于M，连接BM，
，
，平面ADC，
平面SDC，
平面
平面BDC，
又，
平面
平面BDC，
所以
平面BCD，
所以
是AB与平面BCD所成的角，
在
中，
，
，
在
中，
．
直线AB与平面BCD所成角的正弦值为．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
