题目内容
(本题满分12分)
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足cos=,·=3.
(1)求△ABC的面积;
(2)若c=1,求a的 值.
值.
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足cos=,·=3.
(1)求△ABC的面积;
(2)若c=1,求a的
 值.
值.(1)S△ABC=bcsinA=2.
(2)a=2.
(2)a=2.
解:(1) ∵cos=,
∴cosA=2cos2-1=,sinA=. …………………………2分
又由·=3,得bccosA=3,所以bc=5. …………………………4分
因此S△ABC=bcsinA=2. …………………………6分
(2 )由(1)知,bc=5,又c=1,所以b=5, …………………………8
)由(1)知,bc=5,又c=1,所以b=5, …………………………8 分
分
由余弦定理,得a2=b2+c2-2bccosA=20,…………………………10分
∴a=2. …………………………12分
∴cosA=2cos2-1=,sinA=. …………………………2分
又由·=3,得bccosA=3,所以bc=5. …………………………4分
因此S△ABC=bcsinA=2. …………………………6分
(2
 )由(1)知,bc=5,又c=1,所以b=5, …………………………8
)由(1)知,bc=5,又c=1,所以b=5, …………………………8 分
分由余弦定理,得a2=b2+c2-2bccosA=20,…………………………10分
∴a=2. …………………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是角
是角 所对的边,且满足
所对的边,且满足 .
. 的大小;
的大小; ,求
,求 的最小值.
的最小值. (米)是时间
(米)是时间 (
( ,单位:小时)的函数,记作
,单位:小时)的函数,记作 .下表是某日
.下表是某日 各时刻记录的浪高数据:
各时刻记录的浪高数据:




 的图象.
的图象.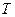 ,振幅
,振幅 及函数表达式;
及函数表达式; ?
? 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,已知
,已知 ,
,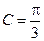 .
. ,求
,求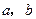 ;
;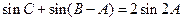 ,求
,求 中,若
中,若 ,且
,且 ,则
,则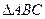 中,若有
中,若有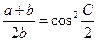 ,则
,则 ,则关于△ABC的两个判断“①一定锐角三角形 ②一定是等腰三角形”中( )
,则关于△ABC的两个判断“①一定锐角三角形 ②一定是等腰三角形”中( ) 中,
中,  分别是
分别是 的对边,若
的对边,若 ,则
,则 ,b=4,那么满足条件的△ABC
,b=4,那么满足条件的△ABC