题目内容
设函数
．
（Ⅰ）求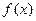
的最小正周期． 
（Ⅱ）若函数
与
的图像关于直线
对称，求当
时的最大值．
．（Ⅰ）求
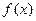的最小正周期． （Ⅱ）若函数
与的图像关于直线对称，求当时的最大值．.u（Ⅰ）8；（Ⅱ）
解：（Ⅰ）=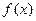
=
=
故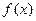的最小正周期为T = 
=8
(Ⅱ)解法一：在的图象上任取一点
，它关于的对称点
.
由题设条件，点在的图象上，从而
=
=
当
时，
，因此在区间
上的最大值为 
;
解法二：因区间关于x = 1的对称区间为
，且与的图象关于
x = 1对称，故在上的最大值为在上的最大值.
由（Ⅰ）知＝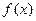
当
时，
,因此在上的最大值为 .
==
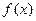=故
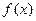的最小正周期为T = =8(Ⅱ)解法一：在
的图象上任取一点，它关于的对称点 .由题设条件，点
在的图象上，从而==当
时，，因此在区间上的最大值为 ;解法二：因区间
关于x = 1的对称区间为，且与的图象关于x = 1对称，故
在上的最大值为在上的最大值.由（Ⅰ）知
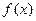＝当
时，,因此在上的最大值为 . 
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，不等式
成立，则实数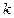
的取值范围是_______________.
。
的周期；
上的减区间；
，
，求
的值。
（
，
）为偶函数，
图象的两相邻对称轴间的距离为
．
的值；
个单位后，得到函数
的图象，求
的单调递减区间．
为增函数
在第一象限为增函数
为奇函数
=
