题目内容
(本题满分10分)选修4 -4 :坐标系与参数方程
将圆 上各点的纵坐标压缩至原来的
上各点的纵坐标压缩至原来的 ,所得曲线记作C;将直线3x-2y-8=0
,所得曲线记作C;将直线3x-2y-8=0
绕原点逆时针旋转90°所得直线记作l
.(I)求直线l与曲线C的方程;
(II)求C上的点到直线l的最大距离.
.(I) 曲线C: ;直线l :
;直线l :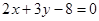 ;(II)
;(II) 。
。
解析试题分析:(Ⅰ)设曲线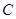 上任一点为
上任一点为 ,则
,则 在圆
在圆 上,
上,
于是 即
即 .
.
直线 的极坐标方程为
的极坐标方程为 ,将其记作
,将其记作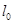 ,
,
设直线上任一点为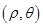 ,则点
,则点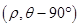 在
在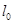 上,
上,
于是 ,即:
,即: ,
,
故直线的方程为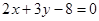 ; …5分
; …5分
(Ⅱ)设曲线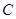 上任一点为
上任一点为 ,
,
它到直线的距离为 ,
,
其中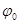 满足:
满足: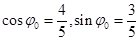 .
.
∴当 时,
时, . …10分
. …10分
考点:直线的极坐标方程;直线与椭圆的位置关系;椭圆的标准方程。
点评:本题主要考查了直线与椭圆的极坐标方程的灵活应用。考查了学生分析问题的能力及数学化归思想.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是( )
| A.总偏差平方和 | B.残差平方和 | C.回归平方和 | D.相关指数R2 |
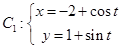 (
(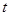 为参数),
为参数),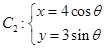 (
(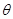 为参数).
为参数).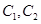 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;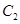 的左顶点且倾斜角为
的左顶点且倾斜角为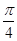 的直线
的直线 交曲线
交曲线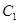 于
于 两点,求
两点,求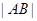 .
. 的极坐标方程为
的极坐标方程为 ,以极点为原点,极轴为轴的正半轴建立直角坐标系,直线
,以极点为原点,极轴为轴的正半轴建立直角坐标系,直线 的参数方程
的参数方程
 得到曲线
得到曲线 ,在曲线
,在曲线 上求一点
上求一点 ,使点
,使点 .
. ,求
,求 的最大值.
的最大值. 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数),若以直角坐标系
为参数),若以直角坐标系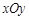 的
的 点为极点,
点为极点,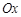 为极轴,且长度单位相同,建立极坐标系,得曲线
为极轴,且长度单位相同,建立极坐标系,得曲线 的极坐标方程为
的极坐标方程为 .直线
.直线 两点,求
两点,求 .
. 坐标是
坐标是 ,曲线
,曲线 的方程为
的方程为 ;以极点为坐标原点,极轴为
;以极点为坐标原点,极轴为 轴的正半轴建立平面直角坐标系,斜率是
轴的正半轴建立平面直角坐标系,斜率是 的直线
的直线 经过点
经过点 、
、 ,并求
,并求 的值.
的值.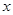 轴的正半轴重合.直线的参数方程是
轴的正半轴重合.直线的参数方程是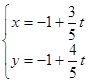 (
(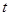 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 .
. 两点,求
两点,求