题目内容
(本小题满分12分)已知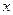 满足不等式
满足不等式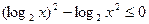 ,求函数
,求函数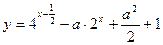 (
(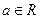 )的最小
)的最小 值.
值.
解:解不等式 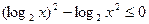 ,得
,得 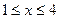 ,
,
所以 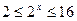 …(3分)
…(3分) …(6分)
…(6分)
当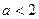 时,
时,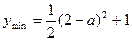 ;…(8分) 当
;…(8分) 当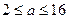 时,
时,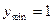 ;…(10分)
;…(10分)
当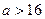 时,
时,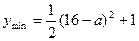 …(12分)
…(12分)
解析

练习册系列答案
相关题目
题目内容
(本小题满分12分)已知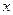 满足不等式
满足不等式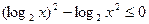 ,求函数
,求函数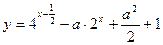 (
(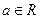 )的最小
)的最小 值.
值.
解:解不等式 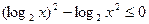 ,得
,得 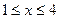 ,
,
所以 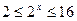 …(3分)
…(3分) …(6分)
…(6分)
当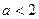 时,
时,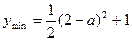 ;…(8分) 当
;…(8分) 当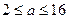 时,
时,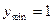 ;…(10分)
;…(10分)
当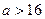 时,
时,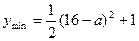 …(12分)
…(12分)
解析
