题目内容
【题目】函数
上任意一点
处的切线
，在其图像上总存在异与点A的点
，使得在B点处的切线
满足
，则称函数具有“自平行性”.下列有关函数的命题：
①函数
具有“自平行性”；②函数
具有“自平行性”；
③函数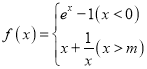
具有“自平行性”的充要条件为实数
；
④奇函数
不一定具有“自平行性”；⑤偶函数
具有“自平行性”.
其中所有叙述正确的命题的序号是（ ）
A.①③④B.①④⑤C.②③④D.①②⑤
【答案】A
【解析】
根据已知中函数具有“自平行性”的定义，逐一分析5个函数是否具有“自平行性”，最后综合讨论结果，可得答案．
解：函数
具有“自平行性”，即对定义域内的任意自变量
，总存在
，使得
．
对于①，
，具有周期性，必满足条件，故①正确；
对于②，
，对任意
，不存在，使得成立，故②错误；
对于③，当
时，
，而
时，
，解得
（舍去）或
，则
，故③正确；
对于④，
，
不符合定义，故④正确；
对于⑤，同④，其导函数为偶函数，故⑤不正确．
故选：
．
练习册系列答案
相关题目
