题目内容
7.若x,y∈R+且x≠y,比较x5+y5与x2y3+x3y2的大小.分析 由已知条件,利用作差法能比较两个式子的大小.
解答 解:∵x,y∈R+且x≠y,
∴(x5+y5)-(x2y3+x3y2)
=(x5-x3y2)-(x2y3-y5)
=x3(x2-y2)-y3(x2-y2)
=(x2-y2)(x3-y3)
=(x-y)(x+y)(x-y)(x2-xy+y2)
=(x-y)2(x+y)(x2-xy+y2)>0,
∴x5+y5>x2y3+x3y2.
点评 本题考查两个式子的大小的比较,是基础题,解题时要认真审题,注意作差法的合理运用.

练习册系列答案
相关题目
15.函数y=sinx-$\sqrt{3}$cosx的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3}{2}π$ | D. | 2π |
16.直线a和面α所成角为60°,b?α,则a,b所成角的范围是( )
| A. | [0°,90°] | B. | [30°,90°] | C. | [60°,90°] | D. | [60°,120°] |
15.有甲乙两个班级进行数学考试,统计成绩后,得到如下列联表:
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”.
参考数据:
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 45 | ||
| 乙班 | 20 | ||
| 合计 | 30 | 105 |
(Ⅱ)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”.
参考数据:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
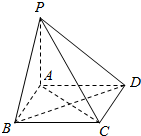 如图所示,四边形ABCD为正方形,PA⊥平面ABCD,则在平面PAB,平面PAD,平面PCD,平面PBC及平面ABCD中,互相垂直的有( )
如图所示,四边形ABCD为正方形,PA⊥平面ABCD,则在平面PAB,平面PAD,平面PCD,平面PBC及平面ABCD中,互相垂直的有( )