Question

（文）已知函数f（x）=x³-x．
（I）求曲线y=f（x）在点M（t，f（t））处的切线方程；
（II）设常数a＞0，如果过点P（a，m）可作曲线y=f（x）的三条切线，求m的取值范围．

Answer 1

分析：（I）求出f′（x），根据切点为M（t，f（t）），得到切线的斜率为f'（t），所以根据斜率和M点坐标写出切线方程即可；
（II）因切线过点（a，m），则存在t使m=（3t²-1）a-2t³，于是过点（a，m）可作曲线y=f（x）的三条切线即为方程m=-2t³+3at²-a（a＞0）有三个相异的实数根．记g（t）=-2t³+3at²-a，求出其导函数=0时t的值，利用t的值分区间讨论导函数的正负得到g（t）的单调区间，利用g（t）的增减性得到g（t）的极值，结合图象，求出m的取值范围．

解答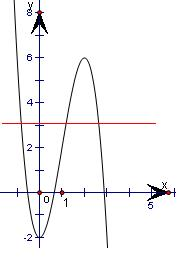：解：（Ⅰ）∵函数f（x）=x³-x，
∴f'（x）=3x²-1．
切线方程为y-f（t）=f'（t）（x-t），
即y=（3t²-1）x-2t³．
（Ⅱ） 已知?关于t的方程m=（3t²-1）a-2t³
即m=-2t³+3at²-a（a＞0）有三个不等实根．
令g（t）=-2t³+3at²-a，则g'（t）=-6t（t-a）．
可知g（t）在（-∞，0）递减，
在（0，a）递增，在（a，+∞）递减，
g（t）的极小值为：g（0）=-a，极大值为g（a）=a³-a．
结合图象知m∈（-a，a³-a）．

点评：考查学生会利用导数研究曲线上某点的切线方程，会利用导数研究函数的增减性得到函数的极值，考查了数形结合的思想．