Question

（文）已知函数f（x）=x³+ax²+bx+2与直线4x-y+5=0切于点P（-1，1）．
（Ⅰ）求实数a，b的值；
（Ⅱ）若x＞0时，不等式f（x）≥mx²-2x+2恒成立，求实数m的取值范围．

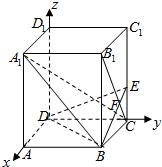
（理） 已知正四棱柱ABCD-A₁B₁C₁D₁底面边长AB=2，侧棱BB₁的长为4，过点B作B₁C的垂线交侧棱CC₁于点E，交线段B₁C于点F．以D为原点，DA、DC、DD₁所在直线分别为x、y、z轴建立空间直角坐标系D-xyz，如图．
（Ⅰ）求证：A₁C⊥平面BED；
（Ⅱ）求A₁B与平面BDE所成角的正弦值的大小．

Answer 1

分析：（文）（1）先对函数进行求导，根据函数f（x）与直线4x-y+5=0切于点P（-1，1），列出方程组即可求出a、b的值．
（2）先分离出参数m：m≤

x3-x2+x

x2

，即m≤x+

1

x

-1令g(x)=x+

1

x

-1（x＞0）只须求得g（x）的最小值即可即可得到m的取值范围．
（理）（Ⅰ）给出各点的坐标，求出两个向量

A1C

，

BD

利用数量积公式即可证得垂直关系，从而即可求解；
（Ⅱ）由（Ⅰ）知

A1C

=(-2，2，-4)是平面BDE的一个法向量．

A1B

=(0，2，-4)，再代入A₁B与平面BDE所成角的余弦公式即可求值．

解答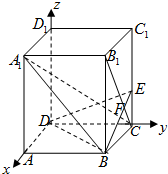：（文）解：（Ⅰ）f′（x）=3x²+2ax+b（2分）
由题意得：

f′(-1)=4 f(-1)=1

即

3-2a+b=4 -1+a-b+2=1

（4分）
解得：a=b=-1．（6分）
（Ⅱ）由（Ⅰ）知：f（x）=x³-x²-x+2
∵f（x）≥mx²-2x+2，
∴mx²≤x³-x²+x．
∵x＞0，
∴m≤

x3-x2+x

x2

，即m≤x+

1

x

-1，（10分）
令g(x)=x+

1

x

-1（x＞0）∴g(x)≥2

x• 1 x

-1=2-1=1，（12分）
当且仅当x=

1

x

时取等号，即x=1时，g（x）_min=1，（14分）
∴m≤1（15分）

（理）解：（Ⅰ）D（0，0，0），A（2，0，0），B（2，2，0），C（0，2，0），A₁（2，0，4），B₁（2，2，4），C₁（0，2，4），D₁（0，0，4）（2分）
设E（0，2，t），则

BE

=(-2，0，t)，

B1C

=(-2，0，-4)．
∵BE⊥B₁C，
∴

BE

•

B1C

=4+0-4t=0．
∴t=1．
∴E（0，2，1），

BE

=(-2，0，1)．（4分）
∵

A1C

=(-2，2，-4)，

DB

=(2，2，0)，
∴

A1C

•

BE

=4+0-4=0且

A1C

•

DB

=-4+4+0=0，（6分）
∴

A1C

⊥

BD

且

A1C

⊥

BE

，
∴

A1C

⊥平面BDE．（8分）
（Ⅱ）由（Ⅰ）知

A1C

=(-2，2，-4)是平面BDE的一个法向量，（9分）
∵

A1B

=(0，2，-4)，
∴cos?

A1C

，

A1B

＞=

A1C • A1B

| A1C || A1B |

=

20

24 20

=

30

6

，（14分）
∴A₁B与平面BDE所成角的正弦值为

30

6

．（16分）

点评：本小题主要考查利用导数研究曲线上某点切线方程、导数在最大值、最小值问题中的应用、向量语言表述线面的垂直、平行关系、用空间向量求直线与平面的夹角等基础知识，考查运算求解能力与转化思想．属于中档题．