题目内容
对于函数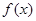 ,若在定义域存在实数
,若在定义域存在实数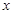 ,满足
,满足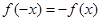 ,则称
,则称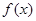 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数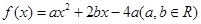 ,试判断
,试判断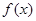 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设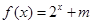 是定义在
是定义在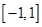 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数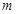 的取值范围.
的取值范围.
(1)是“局部奇函数”;(2)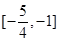 .
.
解析试题分析:(1)本题实质就是解方程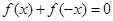 ,如果这个方程有实数解,就说明
,如果这个方程有实数解,就说明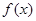 是“局部奇函数”,如果这个方程无实数解,就说明
是“局部奇函数”,如果这个方程无实数解,就说明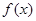 不是“局部奇函数”,易知
不是“局部奇函数”,易知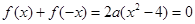 有实数解,因此答案是肯定的;(2)已经明确
有实数解,因此答案是肯定的;(2)已经明确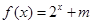 是“局部奇函数”,也就是说方程
是“局部奇函数”,也就是说方程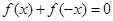 一定有实数解,问题也就变成方程
一定有实数解,问题也就变成方程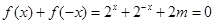 在
在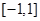 上有解,求参数
上有解,求参数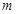 的取值范围,又方程可变形为
的取值范围,又方程可变形为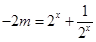 ,因此求
,因此求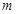 的取值范围,就相当于求函数
的取值范围,就相当于求函数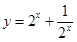
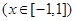 的值域,用换元法(设
的值域,用换元法(设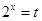 ),再借助于函数
),再借助于函数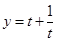 的单调性就可求出.
的单调性就可求出.
试题解析:(1)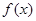 为“局部奇函数”等价于关于
为“局部奇函数”等价于关于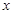 的方程
的方程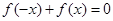 有解.
有解.
即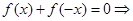
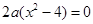 (3分)
(3分)
有解
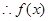 为“局部奇函数”.(5分)
为“局部奇函数”.(5分)
(2)当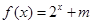 时,
时, 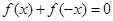 可转化为
可转化为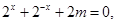 (8分)
(8分)
因为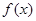 的定义域为
的定义域为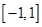 ,所以方程
,所以方程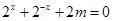 在
在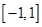 上有解,令
上有解,令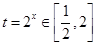 ,(9分)
,(9分)
则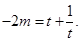
因为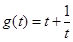 在
在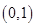 上递减,在
上递减,在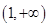 上递增,
上递增,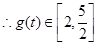 (11分)
(11分)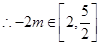 (12分)
(12分)
即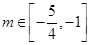 (14分)
(14分)
考点:新定义概念,方程有解求参数取值范围问题.

练习册系列答案
相关题目
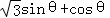 ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.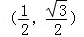 ,求f(θ)的值;
,求f(θ)的值;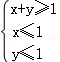 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值. 残骸,我国“雪龙号”科考船于2014年3月26日从港口
残骸,我国“雪龙号”科考船于2014年3月26日从港口 出发,沿北偏东
出发,沿北偏东 角的射线
角的射线 方向航行,而在港口北偏东
方向航行,而在港口北偏东 角的方向上有一个给科考船补给物资的小岛
角的方向上有一个给科考船补给物资的小岛 ,
,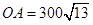 海里,且
海里,且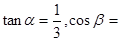
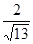 .现指挥部需要紧急征调位于港口
.现指挥部需要紧急征调位于港口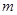 海里的
海里的 处的补给船,速往小岛
处的补给船,速往小岛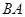 方向全速追赶科考船,并在
方向全速追赶科考船,并在 处相遇.经测算当两船运行的航线与海岸线
处相遇.经测算当两船运行的航线与海岸线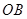 围成的三角形
围成的三角形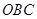 的面积
的面积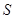 最小时,这种补给方案最优.
最小时,这种补给方案最优.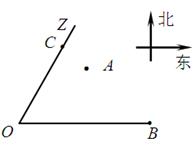
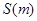 ;
;
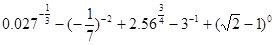
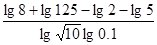
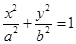 (a>b>0)的离心率为
(a>b>0)的离心率为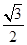 ,过其右焦点F与长轴垂直的弦长为1,
,过其右焦点F与长轴垂直的弦长为1, 万件与年广告费用
万件与年广告费用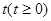 万元满足关系式:
万元满足关系式: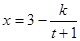 (
( 为常数).若不做广告,则产品的年销售量恰好为1万件.已知2014年生产该产品时,该厂需要先固定投入8万元,并且预计生产每1万件该产品时,需再投入4万元,每件产品的销售价格定为每件产品所需的年平均成本的1.5倍(每件产品的成本包括固定投入和生产再投入两部分,不包括广告促销费用).
为常数).若不做广告,则产品的年销售量恰好为1万件.已知2014年生产该产品时,该厂需要先固定投入8万元,并且预计生产每1万件该产品时,需再投入4万元,每件产品的销售价格定为每件产品所需的年平均成本的1.5倍(每件产品的成本包括固定投入和生产再投入两部分,不包括广告促销费用).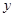 (万元)表示为年广告促销费用
(万元)表示为年广告促销费用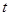 (万元)的函数;
(万元)的函数; 为偶函数.
为偶函数. 的解析式;
的解析式;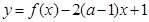 在区间(2,3)上为单调函数,求实数
在区间(2,3)上为单调函数,求实数 的取值范围.
的取值范围.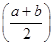 ,
,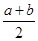 >1.
>1.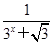 ,求f(-12)+f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)+f(13)的值.
,求f(-12)+f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)+f(13)的值.