题目内容
椭圆c: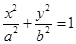 (a>b>0)的离心率为
(a>b>0)的离心率为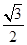 ,过其右焦点F与长轴垂直的弦长为1,
,过其右焦点F与长轴垂直的弦长为1,
(1)求椭圆C的方程;
(2)设椭圆C的左右顶点分别为A,B,点P是直线x=1上的动点,直线PA与椭圆的另一个交点为M,直线PB与椭圆的另一个交点为N,求证:直线MN经过一定点.
(1)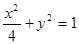 ;(2)证明详见解析
;(2)证明详见解析
解析试题分析:(1)由已知可得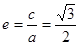 ,
,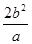 =1,解出a,b即可.
=1,解出a,b即可.
(2)设P(1,t),则直线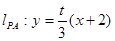 ,联立直线PA方程和椭圆方程可得
,联立直线PA方程和椭圆方程可得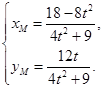 ,同理得到
,同理得到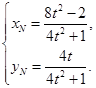 ,由椭圆的对称性可知这样的定点在
,由椭圆的对称性可知这样的定点在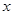 轴,不妨设这个定点为Q
轴,不妨设这个定点为Q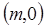 ,由
,由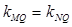 ,求得m的存在即可.
,求得m的存在即可.
试题解析:(1)依题意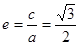
过焦点F与长轴垂直的直线x=c与椭圆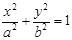
联立解答弦长为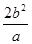 =1, 2分
=1, 2分
所以椭圆的方程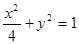 . 4分
. 4分
(2)设P(1,t) ,直线
,直线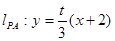 ,联立得:
,联立得: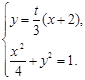
即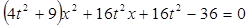 ,
,
可知 所以
所以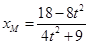 ,
,
则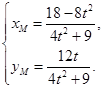 6分
6分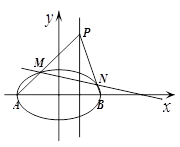
同理得到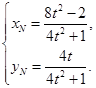 8分
8分
由椭圆的对称性可知这样的定点在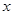 轴,
轴,
不妨设这个定点为Q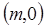 , 10分
, 10分
又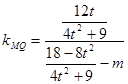 ,
,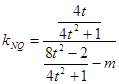 ,
,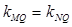 ,
,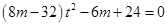 ,
,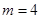 . 12分
. 12分
考点:1.椭圆方程的性质;2.点共线的证法.

练习册系列答案
相关题目
 +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称. ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围. 其中0
其中0
 上恒成立?
上恒成立? 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
 ,当
,当 为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为 ,对称轴与地面垂直,沟深2米,沟中水深1米.
,对称轴与地面垂直,沟深2米,沟中水深1米.

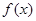 ,若在定义域存在实数
,若在定义域存在实数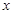 ,满足
,满足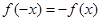 ,则称
,则称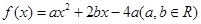 ,试判断
,试判断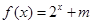 是定义在
是定义在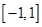 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数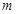 的取值范围.
的取值范围. 满足
满足 ,当
,当 时,
时, ,且
,且 .
. 的值;
的值; 的方程
的方程 有解,求
有解,求 的取值范围.
的取值范围. )元.
)元.