题目内容
下面有四个命题:
(1)各个侧面都是等腰三角形的棱锥是正棱锥;
(2)三条侧棱都相等的棱锥是正棱锥;
(3)底面是正三角形的棱锥是正三棱锥;
(4)顶点在底面上的射影是底面多边形的内心,又是外心的棱锥必是正棱锥.
其中,正确命题的个数是( )
(1)各个侧面都是等腰三角形的棱锥是正棱锥;
(2)三条侧棱都相等的棱锥是正棱锥;
(3)底面是正三角形的棱锥是正三棱锥;
(4)顶点在底面上的射影是底面多边形的内心,又是外心的棱锥必是正棱锥.
其中,正确命题的个数是( )
分析:根据正棱锥的结构特征,底面是正多边形,顶点在底面的射影是底面多边形的中心,依次分析4个命题:对于(1),存在反例,可得(1)错误,对于(2)不符合底面必须是正三角形,也错误;对于(3)不符合三条侧棱长相等,错误,对于(4),可得该棱锥的底面多边形的底面为正多边形,易得顶点在底面上的射影是底面多边形的中心,符合棱锥的定义,故(4)正确,综合可得答案.
解答: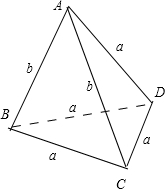 解:根据题意,结合正棱锥的结构特征,依次分析4个命题可得:
解:根据题意,结合正棱锥的结构特征,依次分析4个命题可得:
对于(1)、如图:三棱锥A-BCD中,AB=AC=b,AD=CD=BC=BD=a,其每个侧面是等腰三角形,但不是正三棱锥,故(1)错误;
对于(2)、对于正三棱锥,底面必须是正三角形,故(2)错误;
对于(3)、对于正三棱锥,三条侧棱长必须相等,故(3)错误,
对于(4)、该棱锥的底面多边形的内心与外心重合,则其底面为正多边形,则其内心(外心)为底面多边形的中心,则顶点在底面上的射影是底面多边形的中心,符合棱锥的定义,故(4)正确.
只有一个命题正确;
故选A.
 解:根据题意,结合正棱锥的结构特征,依次分析4个命题可得:
解:根据题意,结合正棱锥的结构特征,依次分析4个命题可得:对于(1)、如图:三棱锥A-BCD中,AB=AC=b,AD=CD=BC=BD=a,其每个侧面是等腰三角形,但不是正三棱锥,故(1)错误;
对于(2)、对于正三棱锥,底面必须是正三角形,故(2)错误;
对于(3)、对于正三棱锥,三条侧棱长必须相等,故(3)错误,
对于(4)、该棱锥的底面多边形的内心与外心重合,则其底面为正多边形,则其内心(外心)为底面多边形的中心,则顶点在底面上的射影是底面多边形的中心,符合棱锥的定义,故(4)正确.
只有一个命题正确;
故选A.
点评:本题考查命题真假的判断、涉及三棱锥的结构特征,解题时要认真审题,熟练掌握三棱锥的结构特征是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目