题目内容
2.对一质点的运动过程观测了4次,得到如表所示的数据.| x | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 6 |
(2)求刻画y与x的关系的线性回归方程为$\hat{y}$=1.7x-0.5.
分析 (1)由已知表格中的数据,易得散点图;
(2)先求出横标和纵标的平均数,得到这组数据的样本中心点,利用最小二乘法求出线性回归方程的系数,代入样本中心点求出a的值,写出线性回归方程.
解答 解:(1)满足条件的散点图如下图所示: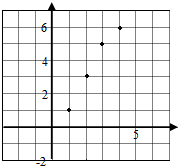
(2)将给出的数据代入公式求解,可求得:$\overline{x}$=$\frac{1+2+3+4}{4}$=2.5,$\overline{y}$=$\frac{1+3+5+6}{4}$=3.75,
$\sum _{i=1}^{4}$xi2=30,$\sum _{i=1}^{4}$xiyi=46,
∴$\hat{b}$=$\frac{46-4×2.5×3.75}{30-4×{2.5}^{2}}$=1.7,
∴$\hat{a}$=$\overline{y}$-1.7$\overline{x}$=-0.5,
∴所求回归直线方程为$\hat{y}$=1.7x-0.5.
故答案为:$\hat{y}$=1.7x-0.5.
点评 本题考查线性回归方程,考查学生对线性回归方程的理解,属于中档题.

练习册系列答案
相关题目
12.复数z1=1+2i,z2=1-i,则z=$\frac{{z}_{1}•{z}_{2}}{1+i}$在复平面内的对应点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.已知集合A={x|(x-1)2<3x+7,x∈R},B=$\left\{{x\left|{\frac{x}{x+1}≤0}\right.}\right\}$,则A∩B=( )
| A. | [-1,0] | B. | (-1,0) | C. | (-1,0] | D. | [-1,0) |
17.在数列{an}中,a1=-2,an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$,则a2014=( )
| A. | -2 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 3 |
7.在腰长为2的等腰直角三角形内任取一点,使得该点到此三角形的直角顶点的距离大于1的概率为( )
| A. | $\frac{π}{16}$ | B. | $\frac{π}{8}$ | C. | $1-\frac{π}{8}$ | D. | $1-\frac{π}{16}$ |