题目内容
 函数y=f(x)是定义在R上的偶函数,且f(-1+x)=f(-1-x),当x∈[-2,-1]时,f(x)=t(x+2)3-t(x+2)(t∈R),记函数y=f(x)的图象在
函数y=f(x)是定义在R上的偶函数,且f(-1+x)=f(-1-x),当x∈[-2,-1]时,f(x)=t(x+2)3-t(x+2)(t∈R),记函数y=f(x)的图象在 处的切线为l,
处的切线为l, .
.(Ⅰ)求y=f(x)在[0,1]上的解析式;
(Ⅱ)点列B1(b1,2),B2(b2,3),…,Bn(bn,n+1)在l上,A1(x1,0),A2(x2,0),…,An(xn,0)依次为x轴上的点,如图,当n∈N*时,点An,Bn,An+1构成以AnAn+1为底边的等腰三角形.若x1=a(0<a<1),求数列{xn}的通项公式;
(Ⅲ)在(Ⅱ)的条件下,是否存在实数a使得数列{xn}是等差数列?如果存在,写出a的一个值;如果不存在,请说明理由.
【答案】分析:(Ⅰ)由函数y=f(x)是定义在R上的偶函数和f(-1+x)=f(-1-x)变形可得f(-1+x)=f(-1-x)=f(1+x),得到f(x)是周期为2的函数,取x∈[0,1],则有x-2∈[-2,-1],可化简f(x),最后由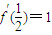 ,求得t,从而得到f(x).
,求得t,从而得到f(x).
(Ⅱ)在(I)下,求得切线的方程“B1(b1,2),B2(b2,3),Bn(bn,n+1)在l上”求得bn“点An,Bn,An+1构成以AnAn+1为底边的等腰三角形”求得xn+xn+1=2bn=2n①,由递推可得xn+1+xn+2=2n+2②两式相减得xn+2-xn=2,间隔项成等差数列.
(Ⅲ)假设{xn}是等差数列,用等差数列的定义可有n-a-n-1+a=常数,不妨设常数为零则有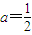 .
.
解答:解:(Ⅰ)∵函数y=f(x)是定义在R上的偶函数,且f(-1+x)=f(-1-x)
∴f(-1+x)=f(-1-x)=f(1+x);
∴y=f(x)是周期为2的函数(1分)
∵当x∈[0,1]时,x-2∈[-2,-1]
∴f(x)=f(x-2)=tx3-tx
由 可知t=-4
可知t=-4
∴f(x)=-4x3+4x,x∈[0,1]
(Ⅱ)∵函数y=f(x)的图象在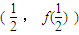 处的切线为l,且
处的切线为l,且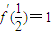 ,
,
∴切线l过点 且斜率为1,
且斜率为1,
∴切线l的方程为y=x+1
∵B1(b1,2),B2(b2,3),Bn(bn,n+1)在l上,有n+1=bn+1即bn=n
∵点An,Bn,An+1构成以AnAn+1为底边的等腰三角形
∴xn+xn+1=2bn=2n①
同理xn+1+xn+2=2n+2②两式相减得xn+2-xn=2
∵x1=a,x2=2-a
∴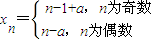
(Ⅲ)假设{xn}是等差数列,则n-a-n-1+a=常数,
不妨设常数为零
则有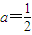 .
.
故存在实数a使得数列{xn}是等差数列.
点评:本题主要考查数列与函数的综合运用,主要涉及了函数的对称性,奇偶性,周期性,数列的定义及其通项,属中档题.
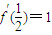 ,求得t,从而得到f(x).
,求得t,从而得到f(x).(Ⅱ)在(I)下,求得切线的方程“B1(b1,2),B2(b2,3),Bn(bn,n+1)在l上”求得bn“点An,Bn,An+1构成以AnAn+1为底边的等腰三角形”求得xn+xn+1=2bn=2n①,由递推可得xn+1+xn+2=2n+2②两式相减得xn+2-xn=2,间隔项成等差数列.
(Ⅲ)假设{xn}是等差数列,用等差数列的定义可有n-a-n-1+a=常数,不妨设常数为零则有
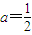 .
.解答:解:(Ⅰ)∵函数y=f(x)是定义在R上的偶函数,且f(-1+x)=f(-1-x)
∴f(-1+x)=f(-1-x)=f(1+x);
∴y=f(x)是周期为2的函数(1分)
∵当x∈[0,1]时,x-2∈[-2,-1]
∴f(x)=f(x-2)=tx3-tx
由
 可知t=-4
可知t=-4∴f(x)=-4x3+4x,x∈[0,1]
(Ⅱ)∵函数y=f(x)的图象在
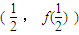 处的切线为l,且
处的切线为l,且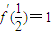 ,
,∴切线l过点
 且斜率为1,
且斜率为1,∴切线l的方程为y=x+1
∵B1(b1,2),B2(b2,3),Bn(bn,n+1)在l上,有n+1=bn+1即bn=n
∵点An,Bn,An+1构成以AnAn+1为底边的等腰三角形
∴xn+xn+1=2bn=2n①
同理xn+1+xn+2=2n+2②两式相减得xn+2-xn=2
∵x1=a,x2=2-a
∴
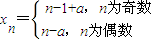
(Ⅲ)假设{xn}是等差数列,则n-a-n-1+a=常数,
不妨设常数为零
则有
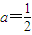 .
.故存在实数a使得数列{xn}是等差数列.
点评:本题主要考查数列与函数的综合运用,主要涉及了函数的对称性,奇偶性,周期性,数列的定义及其通项,属中档题.

练习册系列答案
相关题目
 如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.