题目内容
关于函数y=f(x),有下列命题:①若a∈[-2,2],则函数f(x)=
| x2+ax+1 |
②若f(x)=log
| 1 |
| 2 |
| 3 |
| 2 |
③(理)若f(x)=
| 1 |
| x2-x-2 |
| lim |
| x→2 |
(文)若f(x)=
| 1 |
| x2-x-2 |
④定义在R的函数f(x),且对任意的x∈R都有:f(-x)=-f(x),f(1+x)=f(1-x),则4是y=f(x)的一个周期.
其中真命题的编号是
分析:①根据题意知设g(x)=x2+ax+1为开口向上的二次函数,当△≤0时,x2+ax+1≥0,f(x)有意义,解出△≤0求出a的解集即可;
②f(x)为对数函数,底数为
<1,为单调递减函数,作出判断;③先化简(x-2)f(x)=
,对其求极限得
,得到答案错误;④根据题意可知f(x)为奇函数,且周期为2,则4是函数的一个周期.正确.
②f(x)为对数函数,底数为
| 1 |
| 2 |
| 1 |
| x+1 |
| 1 |
| 3 |
解答:解:①根据题意知设g(x)=x2+ax+1为开口向上的二次函数,当△≤0即a∈[-2,2]时,x2+ax+1≥0,f(x)有意义,所以此命题为真命题;②f(x)为对数函数,底数为
<1,为单调递减函数,故函数没有递增区间,此命题为假命题;③先化简(x-2)f(x)=
,对其求极限得
,此命题为假命题;.④根据题意可知f(x)为奇函数,且周期为2,则4是函数的一个周期.此命题为真命题.所以真命题的编号为①④
故答案为①④
| 1 |
| 2 |
| 1 |
| x+1 |
| 1 |
| 3 |
故答案为①④
点评:考查学生函数的定义域及其求法的能力,以及函数的周期性、对数函数的单调区间、极限及其运算的能力.

练习册系列答案
相关题目
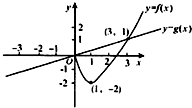 对任意的实数a,b,记max{a,b}=
对任意的实数a,b,记max{a,b}=
|
| A、y=F(x)为奇函数 |
| B、y=F(x)有极大值F(1)且有极小值F(-1) |
| C、y=F(x)的最小值为-2且最大值为2 |
| D、y=F(x)在(-3,0)上不是单调函数 |
 对任意的实数a、b,记
对任意的实数a、b,记 对于任意的实数a、b,记max{a,b}=
对于任意的实数a、b,记max{a,b}= 对于任意的实数a、b,记max
对于任意的实数a、b,记max