题目内容
设 为奇函数,a为常数.
为奇函数,a为常数.(1)求a的值;
(2)若对于区间[3,4]上的每一个x值,不等式
 恒成立,求实数m取值范围.
恒成立,求实数m取值范围.
【答案】分析:(1)根据奇函数的定义,我们可得f(-x)=-f(x),结合已知中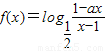 ,可以构造一个关于a的方程,解方程即可求出a的值;
,可以构造一个关于a的方程,解方程即可求出a的值;
(2)构造函数g(x)=f(x)-( )x,判断函数g(x)在区间[3,4]上的单调性,并求出函数g(x)在区间[3,4]上的最小值,进而得到满足条件的实数m取值范围.
)x,判断函数g(x)在区间[3,4]上的单调性,并求出函数g(x)在区间[3,4]上的最小值,进而得到满足条件的实数m取值范围.
解答:解:(1)f(-x)=-f(x),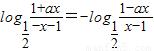 ,可得
,可得
⇒(a2-1)x2=0⇒a=±1
a=1时舍去,故a=-1
(2)f(x)=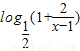
构造g(x)=f(x)-( )x=
)x=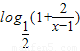 -(
-( )x
)x
易得g(x)在区间[3,4]上单调递增
∴g(x)≥g(3)=-
m<-
∴m∈(-∞,- )
)
点评:本题考查的知识点是对数函数图象与性质的综合应用,及奇函数的性质,其中根据奇函数的性质求出a值,进而得到函数f(x)的解析式是解答本题的关键.
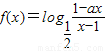 ,可以构造一个关于a的方程,解方程即可求出a的值;
,可以构造一个关于a的方程,解方程即可求出a的值;(2)构造函数g(x)=f(x)-(
 )x,判断函数g(x)在区间[3,4]上的单调性,并求出函数g(x)在区间[3,4]上的最小值,进而得到满足条件的实数m取值范围.
)x,判断函数g(x)在区间[3,4]上的单调性,并求出函数g(x)在区间[3,4]上的最小值,进而得到满足条件的实数m取值范围.解答:解:(1)f(-x)=-f(x),
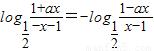 ,可得
,可得
⇒(a2-1)x2=0⇒a=±1
a=1时舍去,故a=-1
(2)f(x)=
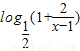
构造g(x)=f(x)-(
 )x=
)x=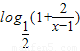 -(
-( )x
)x易得g(x)在区间[3,4]上单调递增
∴g(x)≥g(3)=-

m<-

∴m∈(-∞,-
 )
)点评:本题考查的知识点是对数函数图象与性质的综合应用,及奇函数的性质,其中根据奇函数的性质求出a值,进而得到函数f(x)的解析式是解答本题的关键.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
 为奇函数,a为常数。
为奇函数,a为常数。 的值;并证明
的值;并证明 在区间
在区间 上为增函数;
上为增函数; 上的每一个
上的每一个 的值,不等式
的值,不等式 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. 为奇函数,a为常数。
为奇函数,a为常数。 在区间
在区间 上为增函数;
上为增函数; 上的每一个
上的每一个 的值,不等式
的值,不等式 恒成立,求实数m 的取值范围。
恒成立,求实数m 的取值范围。 为奇函数, a为常数。
为奇函数, a为常数。 在区间
在区间 上为增函数;
上为增函数; 上的每一个
上的每一个 的值,不等式
的值,不等式 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。