题目内容
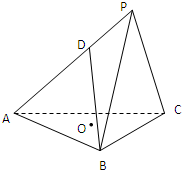 三棱锥P-ABC,底面ABC为边长为2
三棱锥P-ABC,底面ABC为边长为2| 3 |
(Ⅰ)求证DO∥面PBC;
(Ⅱ)求证:BD⊥AC;
(Ⅲ)求面DOB截三棱锥P-ABC所得的较大几何体的体积.
分析:(Ⅰ)连接AO并延长交BC于点E,连接PE、DO,证明DO∥PE,利用直线与平面平行的判定定理直接证明DO∥面PBC;
(Ⅱ)通过证明AC⊥平面DOB,利用直线与平面垂直的性质定理证明BD⊥AC;
(Ⅲ)连接BO并延长交AC于点F,连接DF,则面DOB将三棱锥P-ABC截成三棱锥D-ABF和四棱锥B-DFCP两个几何体,利用体积公式求面DOB截三棱锥P-ABC所得的较大几何体的体积.
(Ⅱ)通过证明AC⊥平面DOB,利用直线与平面垂直的性质定理证明BD⊥AC;
(Ⅲ)连接BO并延长交AC于点F,连接DF,则面DOB将三棱锥P-ABC截成三棱锥D-ABF和四棱锥B-DFCP两个几何体,利用体积公式求面DOB截三棱锥P-ABC所得的较大几何体的体积.
解答: (本小题满分12分)
(本小题满分12分)
证明:(Ⅰ)连接AO并延长交BC于点E,
连接PE、DO.--------------(1分)
∵O为正三角形ABC的中心,
∴AO=2OE,
又AD=2DP,∴DO∥PE,--------------(2分)
∵DO?平面PBC,PE?平面PBC--------------(3分)
∴DO∥面PBC.--------------(4分)
(Ⅱ)∵PB=PC,且E为BC中点,∴PE⊥BC,
又平面PBC⊥平面ABC,∴PE⊥平面ABC.--------------(5分)
由(Ⅰ)知,DO∥PE,∴DO⊥平面ABC,
∴DO⊥AC--------------(6分)
连接BO,则AC⊥BO,
又DO∩BO=O,∴AC⊥平面DOB,--------------(7分)
∴AC⊥BD.--------------(8分)
(Ⅲ)连接BO并延长交AC于点F,连接DF,
则面DOB将三棱锥P-ABC截成三棱锥D-ABF和四棱锥B-DFCP两个几何体.--------------(9分)
VD-ABF=
×S△ABF×DO=
×
×
=
-----------(10分)
VP-ABC=
×S△ABC×PE=
×3
=
--------------(11分)
∴所截较大部分几何体的体积为
.--------------(12分)
 (本小题满分12分)
(本小题满分12分)证明:(Ⅰ)连接AO并延长交BC于点E,
连接PE、DO.--------------(1分)
∵O为正三角形ABC的中心,
∴AO=2OE,
又AD=2DP,∴DO∥PE,--------------(2分)
∵DO?平面PBC,PE?平面PBC--------------(3分)
∴DO∥面PBC.--------------(4分)
(Ⅱ)∵PB=PC,且E为BC中点,∴PE⊥BC,
又平面PBC⊥平面ABC,∴PE⊥平面ABC.--------------(5分)
由(Ⅰ)知,DO∥PE,∴DO⊥平面ABC,
∴DO⊥AC--------------(6分)
连接BO,则AC⊥BO,
又DO∩BO=O,∴AC⊥平面DOB,--------------(7分)
∴AC⊥BD.--------------(8分)
(Ⅲ)连接BO并延长交AC于点F,连接DF,
则面DOB将三棱锥P-ABC截成三棱锥D-ABF和四棱锥B-DFCP两个几何体.--------------(9分)
VD-ABF=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 3 |
VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
∴所截较大部分几何体的体积为
| 2 |
| 3 |
| 3 |
点评:本题考查直线与平面平行的判定定理,直线与平面垂直的判定定理与性质定理的应用,几何体的体积的求法,考查空间想象能力与计算能力.

练习册系列答案
相关题目
已知三棱锥P-ABC的底面是以AB为斜边的等腰直角三角形,且AB=2,PA=PB=PC=2,则该三棱锥的外接球的表面积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
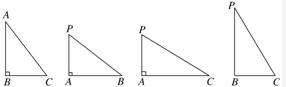 13、下面一组图形为三棱锥P-ABC的底面与三个侧面.已知AB⊥BC,PA⊥AB,PA⊥AC.
13、下面一组图形为三棱锥P-ABC的底面与三个侧面.已知AB⊥BC,PA⊥AB,PA⊥AC.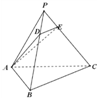 如图,三棱锥P-ABC的底面是正三角形,各条侧棱均相等,∠APB<60°.设点D、E分别在线段PB、PC上,且DE∥BC,记PD=x,△ADE周长为y,则y=f(x)的图象可能是( )
如图,三棱锥P-ABC的底面是正三角形,各条侧棱均相等,∠APB<60°.设点D、E分别在线段PB、PC上,且DE∥BC,记PD=x,△ADE周长为y,则y=f(x)的图象可能是( )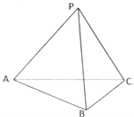 如图,三棱锥P-ABC的底面ABC是以AC为斜边的直角三角形,且顶点P在底面的射影是△ABC外心,设PB=AB=1,BC=
如图,三棱锥P-ABC的底面ABC是以AC为斜边的直角三角形,且顶点P在底面的射影是△ABC外心,设PB=AB=1,BC=