已知购买2个鸡腿和1杯快乐饮料的钱不少于19元.购买1个鸡腿和2杯可乐饮料的钱不少于14元.假设每个鸡腿和每杯饮料的价格都为整数.则购买1个鸡腿和1杯可乐饮料的钱最少需要( )A．10元B．11元C．14元D．16元题目和参考答案——青夏教育精英家教网—

题目内容

20．已知购买2个鸡腿和1杯快乐饮料的钱不少于19元，购买1个鸡腿和2杯可乐饮料的钱不少于14元，假设每个鸡腿和每杯饮料的价格都为整数，则购买1个鸡腿和1杯可乐饮料的钱最少需要（　　）

A．

10元

B．

11元

C．

14元

D．

16元

分析设1个鸡腿的价格为x，1杯可乐饮料的价格为y，建立目标函数和约束条件，利用数形结合进行求解即可．

解答解：设1个鸡腿的价格为x，1杯可乐饮料的价格为y，则购买1个鸡腿和1杯可乐饮料的钱为z，
则z=x+y，x，y∈N，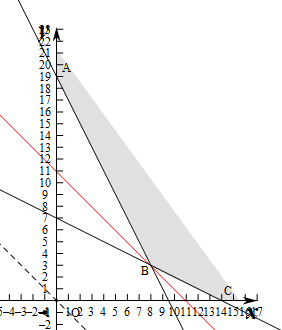
约束条件为$\left\{\begin{array}{l}{x，y∈N}\\{2x+y≥19}\\{x+2y≥14}\end{array}\right.$，
作出不等式组对应的平面区域如图：
由z=x+y得y=-x+z，平移直线y=-x+z，
由图象可知当直线y=-x+z经过点B时，
直线y=-x+z的截距最小，此时z最小．
由$\left\{\begin{array}{l}{2x+y=19}\\{x+2y=14}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=8}\\{y=3}\end{array}\right.$，即B（8，3），代入目标函数z=x+y得z=8+3=11．
即目标函数z=x+y的最小值为11．
故选：B．

点评本题主要考查线性规划的应用，设出变量，建立约束条件，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．

练习册系列答案

中考分类必备全国中考真题分类汇编系列答案

11．将函数y=sinx的图象向右平移$\frac{π}{3}$个单位，再将所得图象上各点横坐标伸长到原来的3倍（纵坐标不变），再将所得图象上各点纵坐标伸长为原来的4倍（横坐标不变），得到函数y=f（x）的图象；
（Ⅰ）写出函数y=f（x）的解析式；
（Ⅱ）求此函数的对称中心的坐标；
（Ⅲ）用五点作图法作出这个函数在一个周期内的图象．

8．在单调递增数列{a_n}中，a₁=2，a₂=4，且a_2n-1，a_2n，a_2n+1成等差数列，a_2n，a_2n+1，a_2n+2成等比数列，n=1，2，3，…．
（Ⅰ）（ⅰ）求证：数列$\{\sqrt{{a_{2n}}}\}$为等差数列；
（ⅱ）求数列{a_n}的通项公式．
（Ⅱ）设数列$\{\frac{1}{a_n}\}$的前n项和为S_n，证明：S_n＞$\frac{4n}{3（n+3）}$，n∈N^*．

15．若f（x）是y=e^x的反函数，且|f（a）|=|f（b）|，a≠b，则a+b的取值范围是（2，+∞）．

5．已知函数f（x）=alog₂x，g（x）=blog₃x（x＞1），其中常数a．b≠0．
（1）证明：用定义证明函数k（x）=f（x）•g（x）的单调性；
（2）设函数φ（x）=m•2^x+n•3^x，其中常数m，n满足m．n＜0，求φ（x+1）＞φ（x）时的x的取值范围．

12．已知函数f（x）=sin（2x+$\frac{3π}{2}$），x∈R，下列结论正确的是（　　）

	A．	函数f（x）的最小正周期为2π		B．	函数f（x）是奇函数
	C．	函数f（x）在[0，$\frac{π}{2}$]上是减函数		D．	函数f（x）的图象关于直线x=$\frac{π}{2}$对称

9．已知函数f（x）=e^x，g（x）=lnx的图象分别与直线y=m交于A，B两点，则满足k＜|AB|恒成立的最大正整数k为参考数据e≈2.718，e^0.1≈1.65，e^0.4≈1.82（　　）

10．小勇是江苏省启东中学2014级高一学生，为他将来读大学的费用做好准备，他父母计划从2014年8月1日起至2016年8月1日期间，每月初定期到银行存款x元（按复利计算），2016年9月1日全部取出，月利率按2%计算，预计大学的费用为6万元，则x=1875．（计算结果精确到元，可参考以下数据：1.02²⁴=1.61，1.02²⁵=1.64，1.02²⁶=1.67）

试题分类