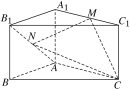
题目内容
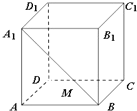
【题目】如图，棱长为1的正方体
中，
是线段
上的动点，则下列结论正确的是（ ）．
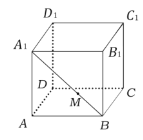
①异面直线
与
所成的角为
②
③三棱锥
的体积为定值
④
的最小值为2．
A.①②③B.①②④C.③④D.②③④
【答案】A
【解析】
①根据异面直线所成的角的定义即可判断；
②由线面垂直的性质即可判断；
③先求得M到平面DCC1D1的距离再利用锥体体积公式求解；
④将问题转化为平面图形中线段AD1的长度，利用余弦定理解三角形解得
即可判断.
①∵
∥BC，
∴异面直线与
所成的角即为BC与所成的角，
可得夹角为
，故①正确；
②连接
，
∵
平面A1BCD1，
平面A1BCD1，
∴
，
故②正确；
③∵
∥平面DCC1D1，
∴线段A1B上的点M到平面DCC1D1的距离都为1,
又△DCC1的面积为定值
,
因此三棱锥MDCC1的体积
为定值,
故③正确；
④将面AA1B与面A1BCD1沿A1B展成平面图形,线段AD1即为AP+PD1的最小值，
在△D1A1A中,∠D1A1A=135°,
利用余弦定理解三角形得
，
故④不正确.
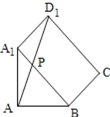
因此只有①②③正确.
故选：A.
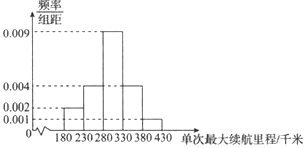
【题目】某花圃为提高某品种花苗质量，开展技术创新活动，在
实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况，分别在实验地随机抽取各50株，对每株进行综合评分，将每株所得的综合评分制成如图所示的频率分布直方图，记综合评分为80及以上的花苗为优质花苗.
（1）求图中
的值，并估计该品种花苗综合评分的平均数（同一组中的数据用该组区间的中点值为代表）；
（2）填写下面的列联表，并判断是否有99%的把握认为优质花苗与培驻外方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附：下面的临界值表仅供参考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
（参考公式：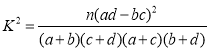
，其中
）
【题目】2017年3月18日，国务院办公厅发布了《生活垃圾分类制度实施方案》，我市环保部门组织了一次垃圾分类知识的网络问卷调查，每位市民都可以通过电脑网络或手机微信平台参与，但仅有一次参加机会工作人员通过随机抽样，得到参与网络问卷调查的100人的得分（满分按100分计）数据，统计结果如下表．
组别 |
|
|
|
|
|
|
女 | 2 | 4 | 4 | 15 | 21 | 9 |
男 | 1 | 4 | 10 | 10 | 12 | 8 |
（1）环保部门规定：问卷得分不低于70分的市民被称为“环保关注者”．请列出
列联表，并判断能否在犯错误的概率不超过
的前提下，认为是否为“环保关注者”与性别有关？
（2）若问卷得分不低于80分的人称为“环保达人”．现在从本次调查的“环保达人”中利用分层抽样的方法随机抽取5名市民参与环保知识问答，再从这5名市民中抽取2人参与座谈会，求抽取的2名市民中，既有男“环保达人”又有女“环保达人”的概率．
附表及公式：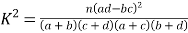
，
．
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
