题目内容
过抛物线y =ax2(a>0)的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是p、q,则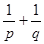 等于 ( )
等于 ( )
A.2a B. 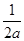 C.4a D.
C.4a D.
【答案】
C
【解析】主要考查抛物线的标准方程及其几何性质、直线与抛物线的位置关系。
解:抛物线y =ax2(a>0)即 ,其焦点为F(0,
,其焦点为F(0, )。依题意设P(
)。依题意设P( ),Q(
),Q(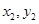 ),直线PQ的方程为
),直线PQ的方程为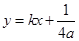 代入y =ax2整理得
代入y =ax2整理得 ,则
,则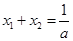 ,
,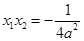 ,
,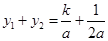 ,
,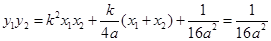 ,而由抛物线定义
,而由抛物线定义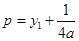 ,
,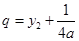 ,所以
,所以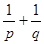 =
=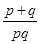 =
= =
=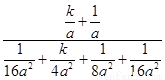 =4ª,故选C。
=4ª,故选C。

练习册系列答案
相关题目
过抛物线y=ax2(a>0)的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是p、q,则
+
等于( )
| 1 |
| p |
| 1 |
| q |
| A、2a | ||
B、
| ||
| C、4a | ||
D、
|