Question

过抛物线y=ax²（a＞0）的焦点F作一直线交抛物线于P、Q两点，若线段PF与FQ的长分别是p、q，则

1

p

+

1

q

等于（　　）

• A、2a
• B、

  1

  2a

• C、4a
• D、

  4

  a

Answer 1

分析：设PQ直线方程是y-

1

4a

=kx，则x₁，x₂是方程ax2=kx+

1

4a

的两根，p=

x 2 1 +(y1- 1 4a )2

=

x 2 1 +(kx1)2

=-x1r，同理q=x₂r．由此可知

1

p

+

1

q

的值．

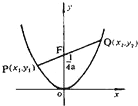解答：解：如图：
设PQ直线方程是y-

1

4a

=kx，
则x₁，x₂是方程ax2=kx+

1

4a

的两根，
p=

x 2 1 +(y1- 1 4a )2

=

x 2 1 +(kx1)2

=-x1r，
其中r=

1+k2

．同理q=x₂r．
从而

1

p

+

1

q

=

p+q

pq

=

(x2-x1)r

-x1x2r2

=

x1-x2

x1x2r

=

(x1+x2)2-4x1x2 -x1x2r

=

( k a )2+4• 1 4a2

1 4a2 •r

=4a．
故选C．

点评：本题考查抛物线的性质和就任，解题时要认真审题，仔细解答．