题目内容
已知椭圆
的左焦点为F，A（-a，0），B（0，b）为椭圆的两个顶点，若F到AB的距离等于
，则椭圆的离心率为（ ）A．
B．
C．
D．
【答案】分析：表示出过A（-a，0），B（0，b）的直线的方程，用截距式直接写出，化为一般式，再由点到直线的距离公式利用距离等于
建立关于a，b的等式，整理变形求离心率．
解答：解：由已知，直线AB的方程：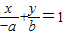
，即bx-ay+ab=0，左焦点为F（-c，0）
F到AB的距离等于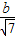
，故有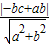
=
，整理得8e2-14e+5=0，解得e=
，或e=
（舍）
故选C．
点评：考查直线方程的两点式与点到直线的距离公式，结合椭圆方程的定义变形出离心率e的方程，求离心率．
建立关于a，b的等式，整理变形求离心率．解答：解：由已知，直线AB的方程：
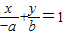，即bx-ay+ab=0，左焦点为F（-c，0）F到AB的距离等于
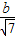，故有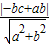=，整理得8e2-14e+5=0，解得e=，或e=（舍）故选C．
点评：考查直线方程的两点式与点到直线的距离公式，结合椭圆方程的定义变形出离心率e的方程，求离心率．
练习册系列答案
期末集结号系列答案
相关题目
的左焦点为F，O为坐标原点。
相切的圆的方程；
轴交于点G，求点G横坐标的取值范围。
的左焦点为F，O为坐标原点．
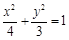的左焦点为F，过点F的直线交椭圆于A、B两点，线段AB的中点为G，AB的中垂线与x轴和y轴分别交于D、E两点．
，求直线AB的斜率；
的左焦点为F，左右顶点分别为A、C，
，其中圆心P的坐标为
．
，求
上，求椭圆的方程．
的左焦点为F，右顶点为A，点B在椭圆上，且
轴，直线AB交
轴于点P。若
，则椭圆的离心率为