题目内容
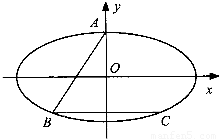
如图,已知椭圆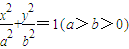 ,梯形ABCD(AB∥CD∥y轴,|AB|>|CD|)内接于椭圆C.
,梯形ABCD(AB∥CD∥y轴,|AB|>|CD|)内接于椭圆C.(I)设F是椭圆的右焦点,E为OF(O为坐标原点)的中点,若直线AB,CD分别经过点E,F,且梯形ABCD外接圆的圆心在直线AB上,求椭圆C的离心率;
(II)设H为梯形ABCD对角线的交点,|AB|=2m,|CD|=2n,|OH|=d,是否存在正实数λ使得
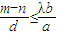 恒成立?若成立,求出λ的最小值,若不存在,请说明理由.
恒成立?若成立,求出λ的最小值,若不存在,请说明理由.
【答案】分析:(I)利用梯形ABCD外接圆的圆心在直线AB上,可得|AE|=|ED|,由此建立方程,求得几何量之间的关系,从而可求椭圆C的离心率;
(II)先确定H在x轴上,再利用韦达定理表示出m-n,进而利用基本不等式,即可求得结论.
解答:解:(I)设F(c,0),则E(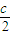 ,0),D(c,
,0),D(c,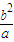 ),A(
),A(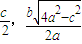 )
)
由题意,梯形ABCD外接圆的圆心在直线AB上,则|AE|=|ED|,所以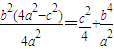
化简得2a2=3c2,所以椭圆的离心率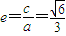 ;
;
(II)根据对称性知识,可得H在x轴上,设H(x,0),则|x|=d
设直线BD的方程为x=ty+x,代入椭圆方程,消去x得(a2+b2t2)y2+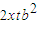 y+
y+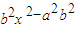 =0
=0
设B(x1,y1),D(x2,y2),则y1+y2=-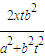
由题意,m=|y1|,n=|y2|,且y1,y2异号
∵m>n>0
∴m-n=|y1+y2|=|- |=
|=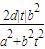
∴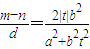 =
=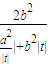 ≤
≤
∴存在正实数λ使得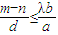 恒成立,且λ的最小值为1.
恒成立,且λ的最小值为1.
点评:本题考查椭圆的离心率,考查存在性问题,考查学生的计算能力,属于中档题.
(II)先确定H在x轴上,再利用韦达定理表示出m-n,进而利用基本不等式,即可求得结论.
解答:解:(I)设F(c,0),则E(
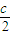 ,0),D(c,
,0),D(c,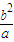 ),A(
),A(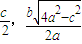 )
)由题意,梯形ABCD外接圆的圆心在直线AB上,则|AE|=|ED|,所以
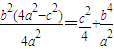
化简得2a2=3c2,所以椭圆的离心率
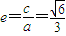 ;
;(II)根据对称性知识,可得H在x轴上,设H(x,0),则|x|=d
设直线BD的方程为x=ty+x,代入椭圆方程,消去x得(a2+b2t2)y2+
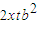 y+
y+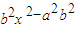 =0
=0设B(x1,y1),D(x2,y2),则y1+y2=-
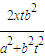
由题意,m=|y1|,n=|y2|,且y1,y2异号
∵m>n>0
∴m-n=|y1+y2|=|-
 |=
|=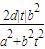
∴
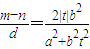 =
=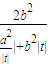 ≤
≤
∴存在正实数λ使得
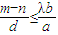 恒成立,且λ的最小值为1.
恒成立,且λ的最小值为1.点评:本题考查椭圆的离心率,考查存在性问题,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 (2012•河北模拟)如图,已知椭圆
(2012•河北模拟)如图,已知椭圆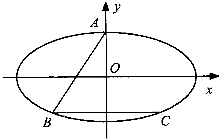 如图,已知椭圆
如图,已知椭圆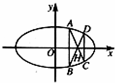 如图,已知椭圆
如图,已知椭圆 ,梯形ABCD(AB∥CD∥y轴,|AB|>|CD|)内接于椭圆C.
,梯形ABCD(AB∥CD∥y轴,|AB|>|CD|)内接于椭圆C.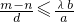 恒成立?若成立,求出λ的最小值,若不存在,请说明理由.
恒成立?若成立,求出λ的最小值,若不存在,请说明理由. 的上顶点为A,直线y=-4交椭圆E于点B,C(点B在点C的左侧),点P在椭圆E上.
的上顶点为A,直线y=-4交椭圆E于点B,C(点B在点C的左侧),点P在椭圆E上.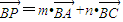 (m,n为实数),求m+n的最大值.
(m,n为实数),求m+n的最大值.