题目内容
如图,已知椭圆 的上顶点为A,直线y=-4交椭圆E于点B,C(点B在点C的左侧),点P在椭圆E上.
的上顶点为A,直线y=-4交椭圆E于点B,C(点B在点C的左侧),点P在椭圆E上.(1)若点P的坐标为(6,4),求四边形ABCP的面积;
(2)若四边形ABCP为梯形,求点P的坐标;
(3)若
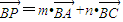 (m,n为实数),求m+n的最大值.
(m,n为实数),求m+n的最大值.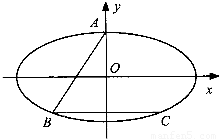
【答案】分析:(1)先求B、C的坐标,再利用四边形ABCP的面积为三角形与梯形面积的和,即可得到结论;
(2)因为ABCP为梯形分情况讨论:①AP平行与BC;②AB平行于CP,则kAB=kCP,求出直线CP的方程,与椭圆方程联立,即可求得P的坐标;
(3)设P(x,y),根据 (m,n为实数),可得x=6m+12n-6,y=9m-4,进而可得m+n,利用三角换元,可求m+n的最大值.
(m,n为实数),可得x=6m+12n-6,y=9m-4,进而可得m+n,利用三角换元,可求m+n的最大值.
解答:解:(1)将y=-4代入椭圆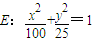 ,可得x=±6,∴B(-6,-4),C(6,-4)
,可得x=±6,∴B(-6,-4),C(6,-4)
∴四边形ABCP的面积为三角形与梯形面积的和
∴S四边形ABCP=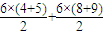 =78
=78
(2)因为ABCP为梯形分情况讨论
①AP平行与BC,则y=5与A重合,所以舍;
②AB平行于CP,则kAB=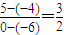 =kCP,
=kCP,
设直线CP的方程为y= x+C,代入(6,4)可得C=-13
x+C,代入(6,4)可得C=-13
∴直线CP的方程为y= x-13,
x-13,
与椭圆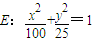 ,联立消元可得5x2-78x+288=0
,联立消元可得5x2-78x+288=0
∴x=6或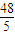
代入直线CP的方程为y= x-13,可得y=-4或
x-13,可得y=-4或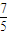
∴P(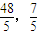 );
);
(3)设P(x,y),∵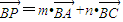 (m,n为实数),
(m,n为实数),
∴(x+6,y+4)=m(6,9)+n(12,0)=(6m+12n,9m)
∴x=6m+12n-6,y=9m-4
∴m=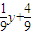 ,n=
,n=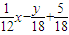
∴m+n=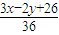
令x=10cosθ,y=5sinθ,∴m+n= cosθ-
cosθ-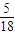 sinθ+
sinθ+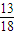 =
=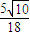 cos(θ+α)+
cos(θ+α)+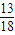 ,所以最大值为
,所以最大值为 +
+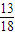 ,
,
∴m+n的最大值为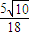 +
+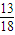 .
.
点评:本题考查四边形面积的计算,考查直线与椭圆的位置关系,考查向量知识的运用,解题的关键是确定坐标之间的关系,属于中档题.
(2)因为ABCP为梯形分情况讨论:①AP平行与BC;②AB平行于CP,则kAB=kCP,求出直线CP的方程,与椭圆方程联立,即可求得P的坐标;
(3)设P(x,y),根据
 (m,n为实数),可得x=6m+12n-6,y=9m-4,进而可得m+n,利用三角换元,可求m+n的最大值.
(m,n为实数),可得x=6m+12n-6,y=9m-4,进而可得m+n,利用三角换元,可求m+n的最大值.解答:解:(1)将y=-4代入椭圆
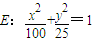 ,可得x=±6,∴B(-6,-4),C(6,-4)
,可得x=±6,∴B(-6,-4),C(6,-4)∴四边形ABCP的面积为三角形与梯形面积的和
∴S四边形ABCP=
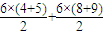 =78
=78(2)因为ABCP为梯形分情况讨论
①AP平行与BC,则y=5与A重合,所以舍;
②AB平行于CP,则kAB=
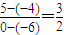 =kCP,
=kCP,设直线CP的方程为y=
 x+C,代入(6,4)可得C=-13
x+C,代入(6,4)可得C=-13∴直线CP的方程为y=
 x-13,
x-13,与椭圆
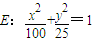 ,联立消元可得5x2-78x+288=0
,联立消元可得5x2-78x+288=0∴x=6或
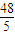
代入直线CP的方程为y=
 x-13,可得y=-4或
x-13,可得y=-4或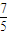
∴P(
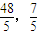 );
);(3)设P(x,y),∵
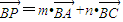 (m,n为实数),
(m,n为实数),∴(x+6,y+4)=m(6,9)+n(12,0)=(6m+12n,9m)
∴x=6m+12n-6,y=9m-4
∴m=
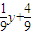 ,n=
,n=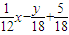
∴m+n=
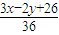
令x=10cosθ,y=5sinθ,∴m+n=
 cosθ-
cosθ-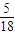 sinθ+
sinθ+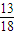 =
=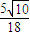 cos(θ+α)+
cos(θ+α)+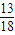 ,所以最大值为
,所以最大值为 +
+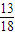 ,
,∴m+n的最大值为
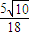 +
+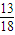 .
.点评:本题考查四边形面积的计算,考查直线与椭圆的位置关系,考查向量知识的运用,解题的关键是确定坐标之间的关系,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

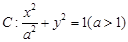 的上顶点为
的上顶点为 ,离心率为
,离心率为 ,若不过点
,若不过点 与椭圆
与椭圆 相交于
相交于 、
、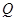 两点,且
两点,且 .
. 的坐标.
的坐标. 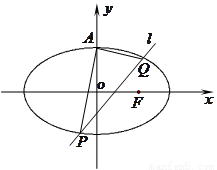
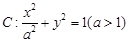 的上顶点为
的上顶点为 ,右焦点为
,右焦点为 ,直线
,直线 与圆
与圆
 相切.
相切. 的方程;
的方程; 与椭圆
与椭圆 、
、 两点,且
两点,且 求证:直线
求证:直线 的坐标.
的坐标.
 的上顶点为
的上顶点为 ,右焦点为
,右焦点为 ,直线
,直线 与圆
与圆
 相切.
相切. 的方程;
的方程; 与椭圆
与椭圆 、
、 两点,且
两点,且 求证:直线
求证:直线 的坐标
的坐标
 (本小题满分12分) 如图,已知椭圆
(本小题满分12分) 如图,已知椭圆