题目内容
已知一点P的坐标是(4,-2),直线L的方程是y-x+5=0,曲线C的方程是| (x+1)2 |
| 2 |
| (y-1)2 |
| 4 |
分析:曲线C是椭圆,中心在(-1,1),其长轴平行于y轴,短轴平行于x轴.设直线L1过点P(4,-2)且垂直于直线L与曲线C相交于点A、B.L1的方程为y+2=-(x-4),解方程组
,可得到直线L1与曲线C的交点.
|
解答:解:曲线C是椭圆,中心在(-1,1),
其长轴平行于y轴,短轴平行于x轴
设直线L1过点P(4,-2)且垂直于直线L与曲线C相交于点A、B.
L1的方程为y+2=-(x-4)即y=-x+2.
欲求L1与曲线C的交点,
解方程组
得
故直线L1与曲线C的交点为A(
,
),B(-1,3).
其长轴平行于y轴,短轴平行于x轴
设直线L1过点P(4,-2)且垂直于直线L与曲线C相交于点A、B.
L1的方程为y+2=-(x-4)即y=-x+2.
欲求L1与曲线C的交点,
解方程组
|
得
|
|
故直线L1与曲线C的交点为A(
| 1 |
| 3 |
| 5 |
| 3 |
点评:本题考查椭圆的方程、性质及其应用,解题时要注意公式的灵活运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
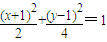 ,求经过P点而与L垂直的直线和曲线C的交点的坐标.
,求经过P点而与L垂直的直线和曲线C的交点的坐标.