题目内容
已知锐角α终边上一点P的坐标是(4sin3,-4cos3),则α=( )
分析:利用任意角三角函数的定义,tanα为终边上点的纵坐标与横坐标之比,得三角等式,再利用诱导公式将两边化为同名函数,且两角处于同一单调区间上,即可解得角α的值
解答:解:依题意:tanα=
=
=-cot3=tan(3-
)
∵α∈(0,
),3-
∈(0,
)
y=tanx在(0,
)上单调
∴α=3-
故选 C
| y |
| x |
| -4cos3 |
| 4sin3 |
| π |
| 2 |
∵α∈(0,
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
y=tanx在(0,
| π |
| 2 |
∴α=3-
| π |
| 2 |
故选 C
点评:本题主要考查了任意角三角函数的定义及其应用,正切函数的定义,诱导公式的运用,简单三角方程的解法等基础知识

练习册系列答案
相关题目
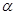 的终边上一点
的终边上一点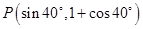 ,则锐角
,则锐角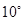 B.
B.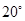 C.
C.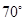 D.
D.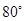
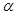 的终边上一点
的终边上一点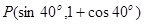 ,则
,则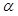 等于( )
等于( )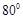 B.
B.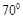 C.
C.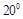 D.
D.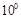
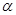 的终边上一点P(
的终边上一点P(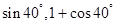 ),则锐角
),则锐角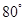 B.
B.
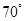 C.
C.
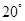 D.
D.