题目内容
把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进。现在投掷一个质地均匀的正四面体,它的四个面上分别写有1、2、3、4四个数字。P从A点出发,按照正四面体底面上数字前进几个分点,转一周之前连续投掷.
(1)求点P恰好返回A点的概率;
(2)在点P转一周恰能返回A点的所有结果中,用随即变量 表示点P能返回A点的投掷次数,求
表示点P能返回A点的投掷次数,求 的分数列和期望.
的分数列和期望.
(1)求点P恰好返回A点的概率;
(2)在点P转一周恰能返回A点的所有结果中,用随即变量
 表示点P能返回A点的投掷次数,求
表示点P能返回A点的投掷次数,求 的分数列和期望.
的分数列和期望.(1)投掷一次正四面体,底面上每个数字的出现都是等可能的,概率为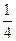 ,则:
,则:
①若投掷一次能返回A点,则底面数字应为4,此时概率为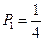 ;
;
②若投掷两次能返回A点,则底面数字一次为(1,3),(3,1),(2,2)三种结果,其概率为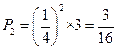 ;
;
③若投三次,则底面数字一次为(1,1,2),(1,2,1),(2,1,1)三种结果,
其概率为 ;
;
④若投四次,则底面数字为(1,1,1,1),其概率为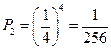 ;
;
(以上每一种情况1分,共4分)
则能返回A点的概率为: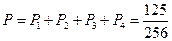 ……………………6分
……………………6分
(2) 的分布列为:
的分布列为:
………………10分
所以,期望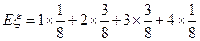
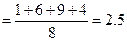 ……………12分
……………12分
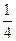 ,则:
,则:①若投掷一次能返回A点,则底面数字应为4,此时概率为
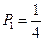 ;
;②若投掷两次能返回A点,则底面数字一次为(1,3),(3,1),(2,2)三种结果,其概率为
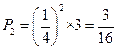 ;
;③若投三次,则底面数字一次为(1,1,2),(1,2,1),(2,1,1)三种结果,
其概率为
 ;
;④若投四次,则底面数字为(1,1,1,1),其概率为
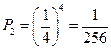 ;
;(以上每一种情况1分,共4分)
则能返回A点的概率为:
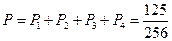 ……………………6分
……………………6分(2)
 的分布列为:
的分布列为: | 1 | 2 | 3 | 4 |
 | 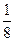 | 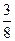 | 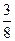 | 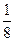 |
………………10分
所以,期望
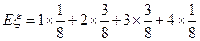
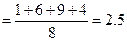 ……………12分
……………12分同答案

练习册系列答案
相关题目

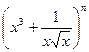 展开式中常数项为84,则n=
展开式中常数项为84,则n= 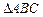 ,其中
,其中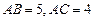 ,现向圆内抛掷一点,则点落在三角形内的概率为
,现向圆内抛掷一点,则点落在三角形内的概率为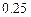 ,则
,则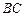 等于( )
等于( )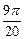
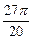
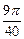
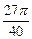
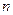 次重复试验得
次重复试验得 到某个事件
到某个事件 发生的频率
发生的频率 ,则随着
,则随着