题目内容
【题目】如图，现要在边长为100m的正方形ABCD内建一个交通“环岛”．以正方形的四个顶点为圆心在四个角分别建半径为xm（x不小于9）的扇形花坛，以正方形的中心为圆心建一个半径为 
m的圆形草地．为了保证道路畅通，岛口宽不小于60m，绕岛行驶的路宽均小于10m． 
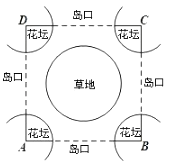
（1）求x的取值范围；（运算中 
取1.4）
（2）若中间草地的造价为a元/m2 ， 四个花坛的造价为 
元/m2 ， 其余区域的造价为 
元/m2 ， 当x取何值时，可使“环岛”的整体造价最低？
【答案】
（1）解：由题意可知，
，
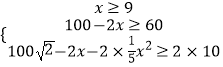解得，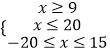 
，
又由 
﹣ 
x2≥10，
解可得﹣14≤x≤14，
即9≤x≤14
（2）解：记“环岛”的整体造价为y元．
则由题意得，
= 
．
令 
，
则 
=﹣4x 
．
由f′（x）=0得，
x=10或x=15．
∴当x=10时，y取最小值．
答：当x=10m时，可使“环岛”的整体造价最低
【解析】（1）根据题目中的不等关系列出关于x的不等式组，求解即可；（2）建立“环岛”的整体造价y与x的关系，然后利用导数求出y取最小值时x的取值即可．
练习册系列答案
相关题目
