题目内容
【题目】已知点![]() 是圆
是圆![]() 上任意一点(
上任意一点(![]() 是圆心),点
是圆心),点![]() 与点
与点![]() 关于原点对称.线段
关于原点对称.线段![]() 的中垂线
的中垂线![]() 分别与
分别与![]() 交于
交于![]() 两点.
两点.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线经过![]() ,与抛物线
,与抛物线![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点.当以
两点.当以![]() 为直径的圆经过
为直径的圆经过![]() 时,求
时,求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据中垂线的性质,![]() ,这样
,这样![]() ,转化为椭圆的定义,根据定义写出椭圆方程;(2)设直线方程,斜率存在时
,转化为椭圆的定义,根据定义写出椭圆方程;(2)设直线方程,斜率存在时![]() 和椭圆方程联立,利用韦达定理写出根与系数的关系,然后根据以
和椭圆方程联立,利用韦达定理写出根与系数的关系,然后根据以![]() 为直径的圆经过
为直径的圆经过![]() 时,有
时,有![]() ,代入坐标关系,最后根据直线方程,根据根与系数的关系求
,代入坐标关系,最后根据直线方程,根据根与系数的关系求![]() ,最后代入抛物线的焦点弦长公式
,最后代入抛物线的焦点弦长公式![]() .
.
试题解析:解:(I)由题意得,F1(﹣1,0),F2(1,0),圆F1的半径为4,且|MF2|=|MP|,
从而|MF1|+|MF2|=|MF1|+|MP|=|PF1|=4>|F1F2|,
∴点M的轨迹是以F1,F2为焦点的椭圆
其中长轴2a=4,得到a=2,焦距2c=2,则短半轴b=![]() ,
,
∴椭圆方程为:![]()
(Ⅱ)当直线l 与x轴垂直时,B1(1,![]() ),B2(1,﹣
),B2(1,﹣![]() ),又F1(﹣1,0),
),又F1(﹣1,0),
此时![]() ,所以以B1B2为直径的圆不经过F1.不满足条件.
,所以以B1B2为直径的圆不经过F1.不满足条件.
当直线l 不与x轴垂直时,设L:y=k(x﹣1)
由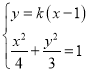 即(3+4k2)x2﹣8k2x+4k2﹣12=0,
即(3+4k2)x2﹣8k2x+4k2﹣12=0,
因为焦点在椭圆内部,所以恒有两个交点.
设B1(x1,y1),B2(x2,y2),则:x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
因为以B1B2为直径的圆经过F1,所以![]() ,又F1(﹣1,0)
,又F1(﹣1,0)
所以(﹣1﹣x1)(﹣1﹣x2)+y1y2=0,即(1+k2)x1x2+(1﹣k2)(x1+x2)+1+k2=0
所以解得k2=![]() ,
,
由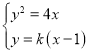 得k2x2﹣(2k2+4)x+k2=0
得k2x2﹣(2k2+4)x+k2=0
因为直线l 与抛物线有两个交点,所以k≠0,
设A1(x3,y3),A2(x4,y4),则:![]() ,x3x4=1
,x3x4=1
所以![]() .
.

 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】某公司过去五个月的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有下列对应数据:
(单位:万元)之间有下列对应数据:
| 2 | 4 | 5 | 6 | 8 |
|
| 40 | 60 | 50 | 70 |
工作人员不慎将表格中![]() 的第一个数据丢失.已知
的第一个数据丢失.已知![]() 对
对![]() 呈线性相关关系,且回归方程为
呈线性相关关系,且回归方程为![]() ,则下列说法:①销售额
,则下列说法:①销售额![]() 与广告费支出
与广告费支出![]() 正相关;②丢失的数据(表中
正相关;②丢失的数据(表中![]() 处)为30;③该公司广告费支出每增加1万元,销售额一定增加
处)为30;③该公司广告费支出每增加1万元,销售额一定增加![]() 万元;④若该公司下月广告投入8万元,则销售
万元;④若该公司下月广告投入8万元,则销售
额为70万元.其中,正确说法有( )
A.1个 B.2个 C.3个 D.4个
【题目】某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
组别 | 频数 | 频率 |
145.5~149.5 | 8 | 0.16 |
149.5~153.5 | 6 | 0.12 |
153.5~157.5 | 14 | 0.28 |
157.5~161.5 | 10 | 0.20 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 |
|
|
合计 |
|
|
(1)求出表中字母![]() 所对应的数值;
所对应的数值;
(2)在给出的直角坐标系中画出频率分布直方图;
(3)估计该校高一女生身高在149.5~165.5![]() 范围内有多少人?
范围内有多少人?