题目内容
15.己知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的上、下顶点分别为A、B,已知点B在直线l:y=一1上,且椭圆的离心率$e=\frac{{\sqrt{3}}}{2}$.(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P是椭圆上异于A、B的任意一点,PQ⊥y轴,Q为垂足,M为线段PQ的中点直线AM交直线,于点C,N为线段BC的中点,求$\overrightarrow{OM}.\overrightarrow{NM}$的值.
分析 (Ⅰ)通过点B在直线l:y=一1上,得b=1,再根据$e=\frac{c}{a}$=$\frac{\sqrt{3}}{2}$及a、c与b之间的关系,易得a2=4,从而可得椭圆的标准方程$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)设P(x0,y0),x0≠0,则点P满足椭圆方程,根据题意,易得M($\frac{{x}_{0}}{2}$,y0)、N($\frac{{x}_{0}}{2(1-{y}_{0})}$,-1),计算$\overrightarrow{OM}•\overrightarrow{NM}$即可•
解答 解:(Ⅰ)∵$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$且点B在直线l:y=一1上,
∴b=1,
又∵$e=\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,a2-c2=b2=1
∴a2=4,
∴椭圆的标准方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)设P(x0,y0),x0≠0,则Q(0,y0),且$\frac{{{x}_{0}}^{2}}{4}+{{y}_{0}}^{2}=1$,
∵M为线段PQ的中点,∴M($\frac{{x}_{0}}{2}$,y0),
∵A(0,1),∴直线AM的方程为:$y=\frac{2({y}_{0}-1)}{{x}_{0}}x+1$,
令y=-1,得C($\frac{{x}_{0}}{1-{y}_{0}}$,-1),
∵B(0,-1),N为线段BC的中点,∴N($\frac{{x}_{0}}{2(1-{y}_{0})}$,-1),
∵$\overrightarrow{NM}$=($\frac{{x}_{0}}{2}$-$\frac{{x}_{0}}{2(1-{y}_{0})}$,y0+1),$\overrightarrow{OM}$=($\frac{{x}_{0}}{2}$,y0),
∴$\overrightarrow{OM}•\overrightarrow{NM}$=$\frac{{x}_{0}}{2}$($\frac{{x}_{0}}{2}$-$\frac{{x}_{0}}{2(1-{y}_{0})}$)+y0(y0+1)
=$\frac{{{x}_{0}}^{2}}{4}-\frac{{{x}_{0}}^{2}}{4(1-{y}_{0})}+{{y}_{0}}^{2}+{y}_{0}$
=$\frac{{{x}_{0}}^{2}}{4}+{{y}_{0}}^{2}$-$\frac{{{x}_{0}}^{2}}{4(1-{y}_{0})}$+y0
=1-(1+y0)+y0
=0•
点评 本题考查椭圆方程,中点坐标公式,向量数量积的运算,注意解题方法的积累,属于中档题.

| A. | $({0,\frac{1}{e}})$ | B. | $({\frac{lg2}{2},\frac{lge}{e}})$ | C. | $({\frac{lg2}{2},e})$ | D. | $({0,\frac{lg2}{2}})$ |
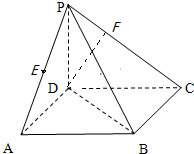 已知:如图在四梭椎P-ABCD中PD垂直于正方形ABCD所在的平面,E是AP的中点.
已知:如图在四梭椎P-ABCD中PD垂直于正方形ABCD所在的平面,E是AP的中点. 如图,⊙O1与⊙O2交于C、D两点,AB为⊙O1的直径,连接AC并延长交⊙O2于点E,连接AD并延长交⊙O2于点F,连接FE并延长交AB的延长线于点G.
如图,⊙O1与⊙O2交于C、D两点,AB为⊙O1的直径,连接AC并延长交⊙O2于点E,连接AD并延长交⊙O2于点F,连接FE并延长交AB的延长线于点G.