题目内容
已知平面向量| α |
| β |
| α |
| 0 |
| α |
| β |
| β |
| α |
| β |
| α |
| α |
分析：画出满足条件的图形，分别用
、
表示向量
与
，由
与
-
的夹角为120°，易得B=60°，再于|
|=1，利用正弦定理，易得|
|的取值范围．
| AB |
| AC |
| α |
| β |
| α |
| β |
| α |
| β |
| α |
解答：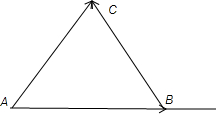
解：令用
=
、
=
，如下图所示：
则由
=
-
，
又∵
与
-
的夹角为120°，
∴∠ABC=60°
又由AC=|
|=1
由正弦定理
=
得：
|
|=
sinC≤
∴|
|∈（0，
]
故|
|的取值范围是（0，
]
故答案：（0，
]
解：令用| AB |
| α |
| AC |
| β |
则由
| BC |
| β |
| α |
又∵
| α |
| β |
| α |
∴∠ABC=60°
又由AC=|
| β |
由正弦定理
|
| ||
| sinC |
|
| ||
| sin60° |
|
| α |
2
| ||
| 3 |
2
| ||
| 3 |
∴|
| α |
2
| ||
| 3 |
故|
| α |
2
| ||
| 3 |
故答案：（0，
2
| ||
| 3 |
点评：本题主要考查了平面向量的四则运算及其几何意义，突出考查了对问题的转化能力和数形结合的能力，属中档题．
练习册系列答案
阶梯计算系列答案
相关题目
已知平面向量
=（1，-3），
=（4，-2），λ
+
与
垂直，则λ是（ ）
| a |
| b |
| a |
| b |
| a |
| A、-1 | B、1 | C、-2 | D、2 |
已知平面向量
，
满足|
|=1，|
|=2，
与
的夹角为60°，则“m=1”是“(
-m
)⊥
”的（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |