题目内容
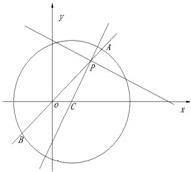 如图,圆C:x2+y2-2x-8=0内有一点P(2,2),过点p作直线l交圆于A,B两点.
如图,圆C:x2+y2-2x-8=0内有一点P(2,2),过点p作直线l交圆于A,B两点.
(1)当直线l经过圆心C时,求直线l的方程;
(2)当弦AB被点P平分时,写出直线l方程;
(3)当直线l倾斜角为45°时,求△ABC的面积.
解:(1)∵圆C:(x-1)2+y2=9,∴KCP =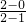 =2,
=2,
又∵点C(1,0)在直线上,∴l的方程为2x-y-2=0,
(2)当弦AB被点P平分时,连CP,则CP⊥AB,
∵KCP=2,KAB=- ,∴l的方程为x+2y-6=0,
,∴l的方程为x+2y-6=0,
(3)∵直线l倾斜角为45°,设直线l的方程为y=x+b,∵直线l过点P,2=2+b,b=0,
∴l的方程为y-x=0,点C到直线l的距离为d=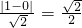 ,
,
由弦长公式可得|AB|=2 =2
=2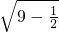 =
= ,
,
∴三角形△ABC的面积是S△ABC= |AB|•d=
|AB|•d=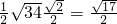 .
.
分析:(1) 先求出直线l的斜率,用点斜式写直线的方程,并化为一般式.
(2)当弦AB被点P平分时,由CP⊥AB,求得AB的斜率,用点斜式求直线方程.
(3)用斜截式设出直线l的方程,点P坐标代入,可得截距的值,由点到直线的距离公式求出点C到直线l的距离,
由弦长公式求|AB|,代入三角形的面积公式进行运算.
点评:本题考查两直线垂直的性质,用点斜式、斜截式求直线的方程,点到直线的距离公式以及弦长公式的应用.
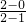 =2,
=2,又∵点C(1,0)在直线上,∴l的方程为2x-y-2=0,
(2)当弦AB被点P平分时,连CP,则CP⊥AB,
∵KCP=2,KAB=-
 ,∴l的方程为x+2y-6=0,
,∴l的方程为x+2y-6=0,(3)∵直线l倾斜角为45°,设直线l的方程为y=x+b,∵直线l过点P,2=2+b,b=0,
∴l的方程为y-x=0,点C到直线l的距离为d=
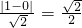 ,
,由弦长公式可得|AB|=2
 =2
=2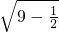 =
= ,
,∴三角形△ABC的面积是S△ABC=
 |AB|•d=
|AB|•d=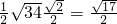 .
.分析:(1) 先求出直线l的斜率,用点斜式写直线的方程,并化为一般式.
(2)当弦AB被点P平分时,由CP⊥AB,求得AB的斜率,用点斜式求直线方程.
(3)用斜截式设出直线l的方程,点P坐标代入,可得截距的值,由点到直线的距离公式求出点C到直线l的距离,
由弦长公式求|AB|,代入三角形的面积公式进行运算.
点评:本题考查两直线垂直的性质,用点斜式、斜截式求直线的方程,点到直线的距离公式以及弦长公式的应用.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3,
如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3, (2013•深圳二模)如图,椭圆E:
(2013•深圳二模)如图,椭圆E: 如图,圆O:x2+y2=
如图,圆O:x2+y2= (2011•武昌区模拟)如图,已知点P是圆
(2011•武昌区模拟)如图,已知点P是圆 如图,圆O:x2+y2=π2内的正弦曲线y=sinx与x轴围成的区域记为M(图中阴影部分),随机往圆O内投一个点A,则点A落在区域M内的概率是( )
如图,圆O:x2+y2=π2内的正弦曲线y=sinx与x轴围成的区域记为M(图中阴影部分),随机往圆O内投一个点A,则点A落在区域M内的概率是( )


