题目内容
如图，圆O：x2+y2=| π | 2 |
分析：先求构成试验的全部区域为圆内的区域的面积，再利用积分知识可得正弦曲线y=sinx与x轴围成的区域记为M的面积，以面积为测度，代入几何概型概率的计算公式可求．
解答：解：构成试验的全部区域为圆内的区域，面积为π3
正弦曲线y=sinx与x轴围成的区域记为M，
根据图形的对称性得：面积为S=2
sinxdx=-2cosx
=4
由几何概率的计算公式可得，随机往圆O内投一个点A，则点A落在区域M内的概率P=
故选D．
正弦曲线y=sinx与x轴围成的区域记为M，
根据图形的对称性得：面积为S=2
| ∫ | π 0 |
| | | π 0 |
由几何概率的计算公式可得，随机往圆O内投一个点A，则点A落在区域M内的概率P=
| 4 | ||
|
故选D．
点评：本题考查几何概型，考查利用积分求解曲面的面积，正确计算面积是关键，属于中档题．
练习册系列答案
相关题目
如图，圆O：x2+y2=π2内的正弦曲线y=sinx与x轴围成的区域记为M（图中阴影部分），随机往圆O内投一个点A，则点A落在区域M内的概率是
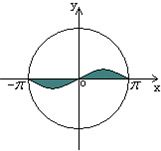如图，圆O：x2+y2=π2内的正弦曲线y=sinx与x轴围成的区域记为M（图中阴影部分），随机往圆O内投一个点A，则点A落在区域M内的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
（2012•吉林二模）如图，圆O：x2+y2=
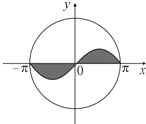如图，圆O：x2+y2=π2内的正弦曲线y=sinx与x轴围成的区域记为M（图中阴影部分），随机往圆O内投一个点A，则点A落在区域M内的概率是（ ）
