题目内容
17.已知函数f(x)=$\left\{\begin{array}{l}2x+b\\{x^2}+({a^2}-4a)x+1\end{array}\right.\begin{array}{l}x≥0\\ x<0\end{array}$,其中a,b∈R.若对任意的非零实数x1,存在唯一的非零实数x2(x1≠x2),使得f(x2)=f(x1)成立,则a+b的取值范围为[1,5].分析 利用分段函数,通过题意推出函数的单调性以及函数值的关系列出方程,求解即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}2x+b\\{x^2}+({a^2}-4a)x+1\end{array}\right.\begin{array}{l}x≥0\\ x<0\end{array}$,x≥0时,函数是增函数;
因为对任意的非零实数x1,存在唯一的非零实数x2(x1≠x2),使得f(x2)=f(x1)成立,
可知x<0时,函数是减函数,并且x=0时,两部分的函数值相等.
可得:1=b,$-\frac{{a}^{2}-4a}{2}≥0$,解得a∈[0,4].
a+b的取值范围为:[1,5].
故答案为:[1,5].
点评 本题考查分段函数的应用,函数与方程的思想的应用,判断函数的单调性是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
5.如图是某几何体的三视图,则这个几何体是( )
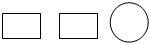

| A. | 圆柱 | B. | 球 | C. | 圆锥 | D. | 棱柱 |
2.集合A={0,1,2,3},B={x∈N|1<x≤5},则A∩B( )
| A. | {2,3} | B. | {2,3,4} | C. | {0,1,2,3,4,5} | D. | {0,1} |
6.先将函数$f(x)=cos(2x-\frac{π}{6})+1$的图象上所有点向右平移$\frac{π}{4}$个单位,再向上平移1个单位后得到函数y=g(x)的图象,则下列正确的是( )
| A. | f(x)的周期是$\frac{π}{2}$ | B. | $f(x+\frac{π}{12})$是奇函数 | ||
| C. | g(x)的图象关于点$(\frac{7π}{12},0)$对称 | D. | g(x)在区间$[0,\frac{π}{3}]$上单调递增 |
 如图是一个空间几何体的三视图,则这个几何体的外接球的体积是$\frac{125\sqrt{2}}{3}π$cm3.
如图是一个空间几何体的三视图,则这个几何体的外接球的体积是$\frac{125\sqrt{2}}{3}π$cm3.