题目内容
3.若a>0,设x,y满足约束条件$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{\frac{x}{3a}+\frac{y}{4a}≤1}\end{array}\right.$,如果z=$\frac{x+2y+3}{x+1}$的最小值为$\frac{3}{2}$,则正数a的值为1.分析 先根据约束条件画出可行域,再利用几何意义求最值,z=$\frac{x+2y+3}{x+1}$中的$\frac{y+1}{x+1}$表示过点(x,y)与(-1.-1)连线的斜率,只需求出可行域内的点与(-1,-1)连线的斜率即可.
解答 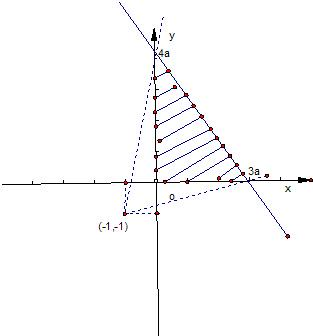 解:∵z=$\frac{x+2y+3}{x+1}$=1+2×$\frac{y+1}{x+1}$,
解:∵z=$\frac{x+2y+3}{x+1}$=1+2×$\frac{y+1}{x+1}$,
而$\frac{y+1}{x+1}$表示过点(x,y)与(-1.-1)连线的斜率,
易知a>0,所以可作出可行域,
z=$\frac{x+2y+3}{x+1}$的最小值为$\frac{3}{2}$,
知$\frac{y+1}{x+1}$的最小值是$\frac{1}{4}$,
即($\frac{y+1}{x+1}$)min=$\frac{0+1}{3a+1}$=$\frac{1}{3a+1}$=$\frac{1}{4}$⇒a=1.
故答案为:1;
点评 本题主要考查了简单的线性规划,以及利用几何意义求最值.涉及到线性规划的题目,每年必考;就此题而言,式子z=$\frac{x+2y+3}{x+1}$的处理应当成为解决本题的关键,一般来说,高考题中的分式结构在处理方式上一般是分离变形,这样其几何意义就表现来了.是中档题.

练习册系列答案
相关题目
15.设P为△ABC所在平面内一点,且$5\overrightarrow{AP}$-2$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{0}$,则△PAB的面积与△ABC的面积之比等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | 不确定 |