题目内容
3.设数列{an}的首项为1,前n项和为Sn,且Sn+1=n2+an+1(n∈N*).(1)求数列{an}的通项公式;
(2)设bn=$\frac{1}{{{a_n}{a_{n+1}}}}$,Tn是数列{bn}的前n项和,求Tn.
分析 (1)利用an=Sn-Sn-1化简求解即可.
(2)化简所求通项公式,利用裂项法求解即可.
解答 解:(1)由 ${S_{n+1}}={n^2}+{a_{n+1}}$,-------------------------------①
则 ${S_n}={({n-1})^2}+{a_n}({n≥2})$-------------②
①-②得:${S_{n+1}}-{S_n}={n^2}-{({n-1})^2}+{a_{n+1}}-{a_n}$,即${a_{n+1}}={n^2}-{({n-1})^2}+{a_{n+1}}-{a_n}$,
得an=2n-1(n≥2),
又a1=1也适合上式,∴an=2n-1. …(6分)
(2)${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{(2n-1)(2n+1)}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,…(9分)
∴Tn=b1+b2+…bn=$\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+…+(\frac{1}{2n-1}-\frac{1}{2n+1})]$=$\frac{1}{2}(1-\frac{1}{2n+1})$
=$\frac{n}{2n+1}$. …(12分)
说明:由${S_{n+1}}={n^2}+{a_{n+1}}$可得${S_n}+{a_{n+1}}={n^2}+{a_{n+1}}$,即${S_n}={n^2}$,亦可求得an=2n-1.
点评 本题考查数列求和,数列的递推关系式的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.直线y=kx+4与圆x2+y2+2kx-2y-2=0交于M,N两点,若点M,N关于直线x+y=0对称,则|MN|等于( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
11.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的表面积是( )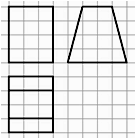

| A. | 42+6$\sqrt{17}$ | B. | 30+6$\sqrt{17}$ | C. | 66 | D. | 44 |
8.在△ABC中,若C=90°,三边为a,b,c,则$\frac{a+b}{c}$的范围是( )
| A. | ($\sqrt{2}$,2) | B. | (1,$\sqrt{2}$] | C. | (0,$\sqrt{2}$] | D. | [$\frac{{\sqrt{2}}}{2}$,$\sqrt{2}$] |
15.直线l的倾斜角为60°,和直线l平行且经过点(-3,2)的直线方程是( )
| A. | y=$\sqrt{3}x+3\sqrt{3}$+2 | B. | y=$\frac{{\sqrt{3}}}{3}x+\sqrt{3}$+2 | C. | y=$\sqrt{3}x-3\sqrt{3}$-2 | D. | y=$\frac{{\sqrt{3}}}{3}x-\sqrt{3}$-2 |
12.若a和b是计算机在区间(0,2)上产生的随机数,那么函数f(x)=lg(ax2+4x+4b)的定义域为R(实数集)的概率为( )
| A. | $\frac{3-2ln2}{4}$ | B. | $\frac{1+2ln2}{4}$ | C. | $\frac{1+ln2}{2}$ | D. | $\frac{1-ln2}{2}$ |
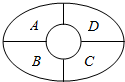 如图某综艺节目现场设有A,B,C,D四个观众席,现有由3不同颜色与2种不同款式组成的6种马甲安排给现场观众,要求每个观众席上的马甲相同,相邻观众席上的马甲的颜色与款式都不相同,则不同的安排方法种数为36.
如图某综艺节目现场设有A,B,C,D四个观众席,现有由3不同颜色与2种不同款式组成的6种马甲安排给现场观众,要求每个观众席上的马甲相同,相邻观众席上的马甲的颜色与款式都不相同,则不同的安排方法种数为36.