题目内容

在△ABC中，a、b、c分别为∠A、∠B、∠C的对边，若A：B：C=1：2：3，则a：b：c=________．


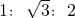
分析：先根据角的关系求出三角的值，再由正弦定理可得到三边的比值．
解答：∵A：B：C=1：2：3∴A=，B=，C=
∴a：b：c=sinA：sinB：sinC=：：1=1：：2
故答案为：1：：2．
点评：本题主要考查正弦定理的应用．正弦定理在三角形的有关题目中应用很广泛，要熟练记忆其定理的内容并要灵活应用．
练习册系列答案
相关题目
在△ABC中，∠A、∠B、∠C所对的边长分别是a、b、c．满足2acosC+ccosA=b．则sinA+sinB的最大值是（　　）
A、
2
2
B、1
C、
2
D、
1+
2
2
在△ABC中，a＜b＜c，B=60°，面积为10
3
cm2，周长为20cm，求此三角形的各边长．
在△ABC中，a，b，c分别为角A，B，C的对边，已知
.
m
=(cos
C
2
，sin
C
2
)，
.
n
=(cos
C
2
，-sin
C
2
)，且
m
•
n
=
1
2
．
（1）求角C；
（2）若a+b=
11
2
，△ABC的面积S=
3
3
2
，求边c的值．
在△ABC中，A，B，C为三个内角，若cotA•cotB＞1，则△ABC是（　　）
已知y=f（x）函数的图象是由y=sinx的图象经过如下三步变换得到的：
①将y=sinx的图象整体向左平移
π
6
个单位；
②将①中的图象的纵坐标不变，横坐标缩短为原来的
1
2
；
③将②中的图象的横坐标不变，纵坐标伸长为原来的2倍．
（1）求f（x）的周期和对称轴；
（2）在△ABC中，a，b，c分别是角A，B，C的对边，且f（C）=2，c=1，ab=2
3
，且a＞b，求a，b的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网