题目内容
已知椭圆 过点
过点 ,离心率
,离心率 ,若点M(x,y)在椭圆C上,则点
,若点M(x,y)在椭圆C上,则点 称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.
称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.(1)求椭圆C的方程;
(2)若椭圆C的右顶点为D,上顶点为E,试探究△OAB的面积与△ODE的面积的大小关系,并证明.
【答案】分析:(1)直接把给出的点的坐标代入椭圆方程,结合离心率及隐含条件a2=b2+c2联立方程组求解a2,b2的值,则椭圆方程可求;
(2)设出A,B的坐标,根据新定义得到P,Q的坐标,当斜率存在时设出直线方程y=kx+m,联立直线和椭圆方程后利用根与系数关系求得x1+x2,x1x2,再由以PQ为直径的圆过原点得到A,B的坐标之间的关系3x1x2+4y1y2=0,转化为横坐标的关系后代入x1+x2,x1x2,即可把直线的斜率用截距表示,然后利用弦长公式求出AB的长度,用点到直线的距离公式求出O点到AB的距离,利用整体运算就能求得三角形OAB的面积,斜率不存在时直线方程可直接设为x=m,和椭圆方程联立求出y2,同样代入3x1x2+4y1y2=0后可直接求出m的值,则三角形面积可求.
解答:解:(1)由已知得: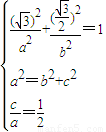 ,即
,即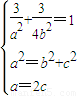 ,
,
解得a2=4,b2=3,所以椭圆方程为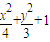 ;
;
(2)设A(x1,y1),B(x2,y2),则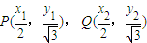
1°当直线l的斜率存在时,设方程为y=kx+m
联立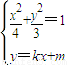 得:(3+4k2)x2+8kmx+4(m2-3)=0.
得:(3+4k2)x2+8kmx+4(m2-3)=0.
则有△=(8km)2-4(3+4k2)×4(m2-3)=48(3+4k2-m2)>0
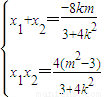 ①
①
由以PQ为直径的圆经过坐标原点O可得:
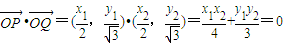 ,即3x1x2+4y1y2=0•
,即3x1x2+4y1y2=0•
把y1=kx1+m,y2=kx2+m代入整理得:
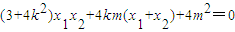 ②
②
将①式代入②式得:3+4k2=2m2,
∵3+4k2>0,∴m2>0,
则△=48m2>0.
又点O到直线y=kx+m的距离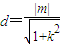 .
.
∴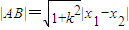 =
=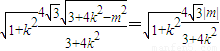 =
=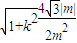
所以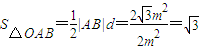
2°当直线l的斜率不存在时,设方程为x=m(-2<m<2)
联立椭圆方程得: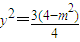
代入3x1x2+4y1y2=0得到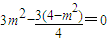 ,即
,即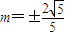 ,y=
,y=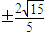 .
.
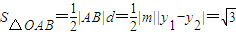
综上:△OAB的面积是定值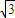 .
.
又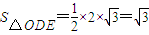 ,所以二者相等.
,所以二者相等.
点评:本题考查了椭圆的标准方程,考查了直线和圆锥曲线的综合,考查了弦长公式的用法,训练了直线和圆锥曲线关系中的设而不求的解题方法,体现了整体运算思想,训练了学生的计算能力,该题是有一定难度问题.
(2)设出A,B的坐标,根据新定义得到P,Q的坐标,当斜率存在时设出直线方程y=kx+m,联立直线和椭圆方程后利用根与系数关系求得x1+x2,x1x2,再由以PQ为直径的圆过原点得到A,B的坐标之间的关系3x1x2+4y1y2=0,转化为横坐标的关系后代入x1+x2,x1x2,即可把直线的斜率用截距表示,然后利用弦长公式求出AB的长度,用点到直线的距离公式求出O点到AB的距离,利用整体运算就能求得三角形OAB的面积,斜率不存在时直线方程可直接设为x=m,和椭圆方程联立求出y2,同样代入3x1x2+4y1y2=0后可直接求出m的值,则三角形面积可求.
解答:解:(1)由已知得:
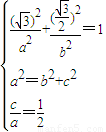 ,即
,即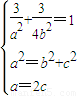 ,
,解得a2=4,b2=3,所以椭圆方程为
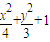 ;
;(2)设A(x1,y1),B(x2,y2),则
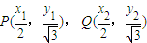
1°当直线l的斜率存在时,设方程为y=kx+m
联立
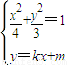 得:(3+4k2)x2+8kmx+4(m2-3)=0.
得:(3+4k2)x2+8kmx+4(m2-3)=0.则有△=(8km)2-4(3+4k2)×4(m2-3)=48(3+4k2-m2)>0
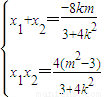 ①
①由以PQ为直径的圆经过坐标原点O可得:
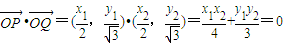 ,即3x1x2+4y1y2=0•
,即3x1x2+4y1y2=0•把y1=kx1+m,y2=kx2+m代入整理得:
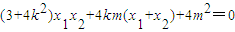 ②
②将①式代入②式得:3+4k2=2m2,
∵3+4k2>0,∴m2>0,
则△=48m2>0.
又点O到直线y=kx+m的距离
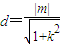 .
.∴
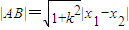 =
=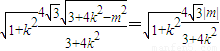 =
=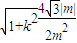
所以
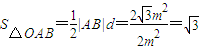
2°当直线l的斜率不存在时,设方程为x=m(-2<m<2)
联立椭圆方程得:
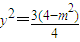
代入3x1x2+4y1y2=0得到
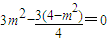 ,即
,即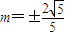 ,y=
,y=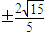 .
.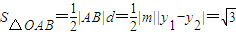
综上:△OAB的面积是定值
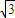 .
.又
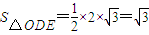 ,所以二者相等.
,所以二者相等.点评:本题考查了椭圆的标准方程,考查了直线和圆锥曲线的综合,考查了弦长公式的用法,训练了直线和圆锥曲线关系中的设而不求的解题方法,体现了整体运算思想,训练了学生的计算能力,该题是有一定难度问题.

练习册系列答案
相关题目
 过点
过点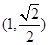 ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 、
、 .点
.点 为直线
为直线 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线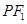 和
和 与椭圆的交点分别为
与椭圆的交点分别为 、
、 和
和 、
、 ,
, 为坐标原点.设直线
为坐标原点.设直线 、
、 .
.
 ;
; 上是否存在点
上是否存在点 、
、 、
、 、
、 的斜率
的斜率 、
、 、
、 、
、 满足
满足 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点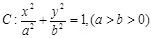 过点
过点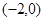 ,离心率
,离心率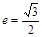 ,
, 的直线
的直线 与椭圆C交于
与椭圆C交于 两点,且以
两点,且以 为直径的圆过原点,试求直线
为直径的圆过原点,试求直线 过点
过点 ,离心率为
,离心率为 ,圆
,圆 的圆心为坐标原点,直径为椭圆的短轴,圆
的圆心为坐标原点,直径为椭圆的短轴,圆 的方程为
的方程为 .过圆
.过圆 作圆
作圆 ,切点为
,切点为 .
. 与圆
与圆 ,当弦
,当弦 最大时,求直线
最大时,求直线 的最值.
的最值. 过点.
过点. ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 、
、 .点
.点 为直线
为直线 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为 、
、 和
和 、
、 ,
, 为坐标原点.
为坐标原点. 、
、 . 证明:
. 证明:

 (本小题满分15分)
(本小题满分15分)