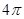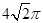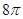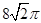题目内容
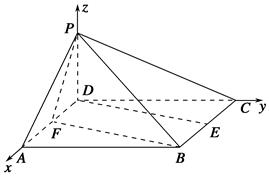
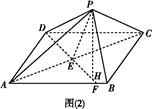
已知四棱锥PABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC,AD的中点.
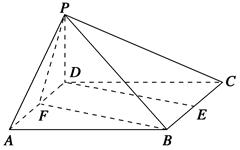
(1)求证:DE∥平面PFB;
(2)已知二面角PBFC的余弦值为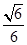 ,求四棱锥PABCD的体积.
,求四棱锥PABCD的体积.

(1)求证:DE∥平面PFB;
(2)已知二面角PBFC的余弦值为
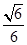 ,求四棱锥PABCD的体积.
,求四棱锥PABCD的体积.(1)见解析(2)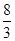
(1)因为E,F分别为正方形ABCD的两边BC,AD的中点,所以BE綉FD,即BEDF为平行四边形,
∴ED∥FB,∵FB?平面PFB,且ED?平面PFB,
∴DE∥平面PFB.
(2)以D为原点,直线DA,DC,DP分别为x,y,z轴建立空间直角坐标系.如图,设PD=a,
可得如下点的坐标P(0,0,a),F(1,0,0),B(2,2,0).
则有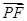 =(1,0,-a),
=(1,0,-a),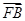 =(1,2,0).
=(1,2,0).
因为PD⊥底面ABCD,所以平面ABCD的一个法向量为m=(0,0,1).
设平面PFB的法向量为n=(x,y,z),
则可得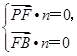 即
即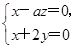 .,
.,
令x=1, 得z=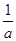 ,y=-
,y=-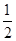 ,
,
所以n=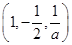 .
.
由已知二面角P-BF-C的余弦值为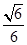 ,
,
所以得cos〈m,n〉=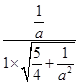 =
=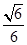 ,
,
∴a=2,∴VP-ABCD=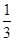 ×2×2×2=
×2×2×2=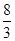
∴ED∥FB,∵FB?平面PFB,且ED?平面PFB,
∴DE∥平面PFB.
(2)以D为原点,直线DA,DC,DP分别为x,y,z轴建立空间直角坐标系.如图,设PD=a,

可得如下点的坐标P(0,0,a),F(1,0,0),B(2,2,0).
则有
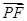 =(1,0,-a),
=(1,0,-a),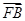 =(1,2,0).
=(1,2,0).因为PD⊥底面ABCD,所以平面ABCD的一个法向量为m=(0,0,1).
设平面PFB的法向量为n=(x,y,z),
则可得
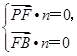 即
即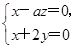 .,
.,令x=1, 得z=
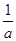 ,y=-
,y=-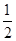 ,
,所以n=
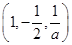 .
.由已知二面角P-BF-C的余弦值为
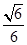 ,
,所以得cos〈m,n〉=
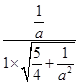 =
=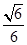 ,
,∴a=2,∴VP-ABCD=
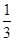 ×2×2×2=
×2×2×2=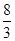

练习册系列答案
相关题目
 AC
AC
 ABC体积的最大值.
ABC体积的最大值. 中,
中,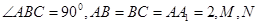 分别是
分别是 的中点.
的中点.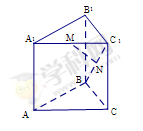
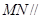 平面
平面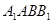 ;
; 的体积.
的体积.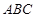 中,
中,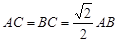 ,
,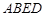 是边长为
是边长为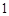 的正方形,平面
的正方形,平面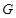 、
、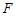 分别是
分别是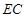 、
、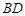 的中点.
的中点.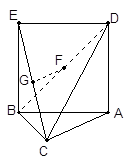
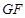 ∥底面
∥底面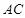 ⊥平面
⊥平面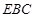 ;
;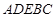 的体积.
的体积.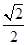 ,
,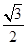 ,
,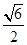 ,则该三棱锥外接球的表面积为( )
,则该三棱锥外接球的表面积为( )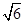 π
π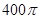
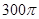
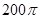
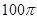
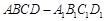 中,点
中,点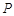 在面对角线
在面对角线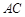 上运动,给出下列四个命题:
上运动,给出下列四个命题: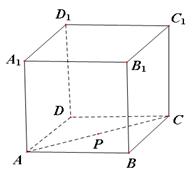
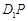 ∥平面
∥平面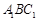 ; ②
; ②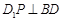 ;
;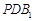 ⊥平面
⊥平面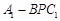 的体
的体 的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( )
的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( )