题目内容
某商品在30天内的销售价格p(单位:元)与时间t(单位:天)的函数关系式为p(t)=
.该商品的日销售量q(单位:件)与时间t(单位:天)的函数关系式q(t)=-t+40(t∈(0,30],t∈N),求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是这30天中的第几天?
|
分析:由已知中销售价格p(单位:元)与时间t(单位:天)的函数关系式和商品的日销售量q(单位:件)与时间t(单位:天)的函数关系式,可得日销售金额为f(t)与时间t(单位:天)的函数关系式,结合二次函数的图象和性质及分段函数最值的求法,可得答案.
解答:解:设日销售金额为f(t)
则f(t)=p(t)q(t)=
即f(t)=
…(4分)
当t∈(0,25),f(t)=-t2+20t+800=-(t-10)2+900
此时f(t)≤f(10)=900…(8分)
当t∈[25,30]时,f(t)=t2-140t+4000=(t-70)2-900
此时f(t)≤f(25)=1125…(12分)
故fmax=f(25)=1125…(14分)
答:在第25天销售额最大,为1125元.…(15分)
则f(t)=p(t)q(t)=
|
即f(t)=
|
当t∈(0,25),f(t)=-t2+20t+800=-(t-10)2+900
此时f(t)≤f(10)=900…(8分)
当t∈[25,30]时,f(t)=t2-140t+4000=(t-70)2-900
此时f(t)≤f(25)=1125…(12分)
故fmax=f(25)=1125…(14分)
答:在第25天销售额最大,为1125元.…(15分)
点评:考查学生根据实际问题选择函数类型的能力,理解分段函数的能力.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
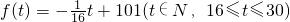 .
.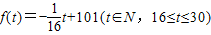 .
.