题目内容
经市场调查,某商品在30天内,其销售量(单位:件)和价格(单位:元)均为时间t(单位:天)的函数,且销售量近似地满足关系g(t)=-t+100(t∈N,0<t≤30),在前15天里价格为f(t)=t+80(t∈N,0<t≤15),在后15天里价格为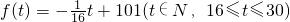 .
.
(1)写出该种商品的日销售额S与时间t的函数关系;
(2)求这种商品的日销售额的最大值.
解:(1)当0<t≤15时,S=g(t)f(t)=(-t+100)(t+80);
当16≤t≤30时,S=g(t)f(t)=(-t+100)(- t+101),
t+101),
所以该种商品的日销售额S与时间t的函数关系为: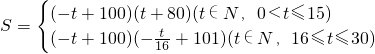 ;
;
(2)当0<t≤15时,S=(-t+100)(t+80)=-(t-10)2+8100.
当t=10时,Smax=8100.
当16≤t≤30时,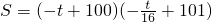 =
=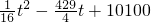 ,
,
易知此时S在[16,30]上递减,所以当t=16时,Smax=8400.
日销售额的最大值为8400元.
综上可得,当t=16时,日销售额的最大值为8400元.
分析:(1)日销售额S=g(t)f(t),分0<t≤15,16≤t≤30两种情况分别表示出来,然后写成分段函数即可;
(2)利用二次函数的性质分别求出S在(0,15],[16,30]上的最大值,然后取其较大者即可;
点评:本题考查函数解析式的求法及二次函数在闭区间上的最值,考查学生在实际问题中的建模能力.
当16≤t≤30时,S=g(t)f(t)=(-t+100)(-
 t+101),
t+101),所以该种商品的日销售额S与时间t的函数关系为:
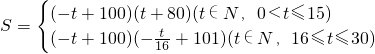 ;
;(2)当0<t≤15时,S=(-t+100)(t+80)=-(t-10)2+8100.
当t=10时,Smax=8100.
当16≤t≤30时,
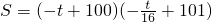 =
=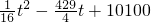 ,
,易知此时S在[16,30]上递减,所以当t=16时,Smax=8400.
日销售额的最大值为8400元.
综上可得,当t=16时,日销售额的最大值为8400元.
分析:(1)日销售额S=g(t)f(t),分0<t≤15,16≤t≤30两种情况分别表示出来,然后写成分段函数即可;
(2)利用二次函数的性质分别求出S在(0,15],[16,30]上的最大值,然后取其较大者即可;
点评:本题考查函数解析式的求法及二次函数在闭区间上的最值,考查学生在实际问题中的建模能力.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
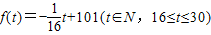 .
.