在△ABC中.①若B=60°.a=10.b=7.则该三角形有且有两解,②若三角形的三边的比是3:5:7.则此三角形的最大角为120°,③若△ABC为锐角三角形.且三边长分别为2.3.x.则x的取值范围是$\sqrt{5}＜x＜\sqrt{13}$．其中正确命题的个数是( )A．0B．1C．2D．3 题目和参考答案——青夏教育精英家教网——

题目内容

12．在△ABC中，
①若B=60°，a=10，b=7，则该三角形有且有两解；
②若三角形的三边的比是3：5：7，则此三角形的最大角为120°；
③若△ABC为锐角三角形，且三边长分别为2，3，x，则x的取值范围是$\sqrt{5}＜x＜\sqrt{13}$．
其中正确命题的个数是（　　）

A．

0

B．

1

C．

2

D．

3

分析根据解三角形的知识，分别对①②③进行判断其正误即可．

解答解：①如图示：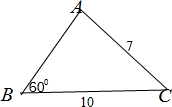
，
由$\frac{a}{sinA}$=$\frac{b}{sinB}$，得：sinA=$\frac{5\sqrt{3}}{7}$，
∴A=arcsin$\frac{5\sqrt{3}}{7}$＞60°，
∴C只能是锐角，该三角形有且只有一个解，
故①错误；
②不妨设：三角形的三边是：a=3，b=5，c=7，
∴∠C最大，由cosC=$\frac{9+25-49}{2×3×5}$=-$\frac{1}{2}$，
∠C=120°，故②正确；
③由cosA＞0，cosB＞0且cosC＞0，结合余弦定理知，正确，
故选：C．

点评本题考查了解三角形问题，考查命题的真假的判断，是一道基础题．

练习册系列答案

国华图书学业测评系列答案

志鸿优化赢在课堂系列答案

作业辅导系列答案

第一课堂课堂作业系列答案

金牌堂堂练系列答案

一本搞定系列答案

同步学典一课多练系列答案

名师金典BFB初中课时优化系列答案

经典密卷系列答案

启智课堂系列答案

相关题目

3．求f（x）=$\frac{\sqrt{1+{x}^{2}}}{\sqrt{1-{x}^{2}}}$的单调递增区间．

4．若正数a，b满足：$\frac{1}{a}+\frac{2}{b}=1$则$\frac{2}{a-1}+\frac{1}{b-2}$的最小值为（　　）

1．已知（x+y+2）ⁿ=a₀₀xⁿ+a₁₀x^n-1+…a_n0+a₁₁x^n-1y+a₂₁x^n-2y+…+a_n1y+a₂₂x^n-2y²+a₃₂x^n-3y²+…a_n2y²+…+a_{（n-1）（n-1）}xy^n-1+a_n（n-1）y^n-1+a_nnyⁿ，（n∈N^*）．
（1）当n=4时，求a₁₁和a₃₂；
（2）是否存在正整数r和n，使得a_r2，a_（r+1）2，a_（r+2）2的比值恰好是3：4：5，若存在，求出r和n，若不存在，请说明理由．

7．已知数列{a_n}的首项a₁=1，且对每个n∈N^*，a_n，a_n+1是方程x²+3nx+b_n=0的两根，则b₁₀=224．

17．下列命题中，正确命题的序号是①④．
①函数y=sin|x|不是周期函数．
②函数y=tanx在定义域内是增函数．
③函数y=|cos2x+$\frac{1}{2}$|的周期是$\frac{π}{2}$．
④y=sin（x+$\frac{5π}{2}$）是偶函数，
⑤函数y=sin（2x+$\frac{π}{3}$）的图象关于点（$\frac{π}{12}$，0）成中心对称图形．

4．抛物线y²=-12x的准线与双曲线$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{2}$=1的两条渐近线所围成的三角形的面积等于$3\sqrt{3}$．

1．已知向量$\overrightarrow a$，$\overrightarrow b$满足|$\overrightarrow a$|=3，|$\overrightarrow b$|=2$\sqrt{3}$，（i）若|$\overrightarrow a$+$\overrightarrow b$|=3$\sqrt{3}$，则向量$\overrightarrow a$，$\overrightarrow b$夹角余弦值为$\frac{\sqrt{3}}{6}$，
（ii）若$\overrightarrow a⊥（\overrightarrow a+\overrightarrow b）$，则$\overrightarrow b$在$\overrightarrow a$方向上的投影为-3．

2．某工厂甲，乙两名工人参加操作技能培训，他们在培训期间参加的8次测试成绩记录如下：
甲95、82、88、81、93、79、84、78
乙83、92、80、95、90、80、85、75
试比较哪个工人的成绩好．