题目内容

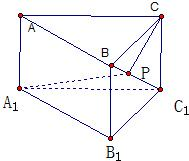精英家教网如图，在直三棱柱ABC-A1B1C1中，底面为直角三角形，∠ABC=90°，AC=6，BC=CC1=
2
，P是BC1上一动点，则CP+PA1的最小值是
 
．
分析：连A1B，沿BC1将△CBC1展开与△A1BC1在同一个平面内，不难看出CP+PA1的最小值是A1C的连线．（在BC1上取一点与A1C构成三角形，因为三角形两边和大于第三边）由余弦定理即可求解．
解答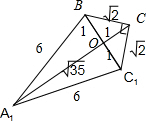：精英家教网解：连A1B，沿BC1将△CBC1展开与△A1BC1在同一个平面内，如图所示，
连A1C，则A1C的长度就是所求的最小值．
通过计算可得AB=6又∠BC1C=45°，BC1=2，
可求得A1C=1+
35

故答案为：1+
35
点评：本题考查棱柱的结构特征，余弦定理的应用，是中档题．
练习册系列答案
相关题目

如图，在直三棱柱AB-A1B1C1中．∠ BAC=90°，AB=AC=AA1 =1．D是棱CC1上的一P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA．

(I)求证：CD=C1D：

(II)求二面角A-A1D-B的平面角的余弦值；　

(Ⅲ)求点C到平面B1DP的距离．

 

 (本小题共l2分)

    如图，在直三棱柱AB-A1B1C1中．∠ BAC=90°，AB=AC=AA1 =1．D是棱CC1上的一[来源:]

P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA．

(I)求证：CD=C1D：

(II)求二面角A-A1D-B的平面角的余弦值；   

(Ⅲ)求点C到平面B1DP的距离．

 

 (本小题共l2分)

    如图，在直三棱柱AB-A1B1C1中．∠ BAC=90°，AB=AC=AA1 =1．D是棱CC1上的一

P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA．

(I)求证：CD=C1D：

(II)求二面角A-A1D-B的平面角的余弦值；   

(Ⅲ)求点C到平面B1DP的距离．

 

 

 
如图，在直三棱柱AB-A1B1C1中，∠ BAC=90°，AB=AC=AA1=1，D是棱CC1上一点，P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA。
（I）求证：CD=C1D；
（II）求二面角A-A1D-B的平面角的余弦值；
（Ⅲ）求点C到平面B1DP的距离

    如图，在直三棱柱AB-A1B1C1中．∠ BAC=90°，AB=AC=AA1 =1．D是棱CC1上的一点，P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA．

(I)求证：CD=C1D：

(II)求二面角A-A1D-B的平面角的余弦值；

(Ⅲ)求点C到平面B1DP的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网